Introduction

“Goma,” which means rubber, gum, or elastic in Spanish, is a two- or three-dimensional finite element program currently being advanced and specialized for the analysis of manufacturing flows and related processes that involve one or more transport fields, i.e., any combination of heat, mass, momentum (solid and fluid) and species transport fields. Specifically, the processes for which Goma is suited are those which contain free or moving boundaries between dissimilar materials or phases. Whether determining the position of an interface whose motion is governed by the underlying physics of the problem, or prescribing the dynamics of a boundary according to user specified kinematics or geometry, the multiphysics approach on which Goma is based allows for rapid convergence to the solution. Unique features which make this possible include: (1) a Lagrangian-Eulerian solid mechanics module for mesh motion, (2) energy and chemical species transport modules incorporating convection, diffusion and reaction, (3) fluid momentum transport modules that are fully and mutually coupled, particularly with the mesh motion module through an analytical Jacobian matrix, (3) a Newton-based solution algorithm (full and modified) which exploits that Jacobian matrix, and (4) a structure which allows for different physical descriptions of different materials in the same problem, i.e., conjugate problems. The scope of potentially accessible problems defined by the interaction and close coupling of the individual field equation sets is partially shown in Figure 1 (note that missing from this figure are the fully coupled, partially saturated porous deformable media module and overall variable density mass balance modules). The analytical Jacobian matrix which provides the coupling facilitates a range of computer-aided nonlinear analyses such as parametric sensitivity (stability), design, and optimization as it provides the building blocks (through chain-rule differentiation) for evaluating sensitivities of process variables to processing conditions.

Goma originated in 1994 from an early version of MP_SALSA (Shadid, et. al., 1995), a finite element program designed to simulate chemically reacting flows in massively-parallel computing environments. As a point-of-departure, Goma was originally extended and adapted to free and moving boundary problems in fluid mechanics, heat transfer, and mass transfer. By virtue of a novel mesh motion algorithm based on Lagrangian solid elasticity, many multiphysics problems involving nonlinear elasticity and viscoplasticity in combination with other transport phenomena are now accessible. The detailed algorithm and underlying physical principles of the moving mesh scheme together with several advanced examples from capillary hydrodynamics, melting and solidification, and polymer processing may be found elsewhere (Sackinger, et. al., 1995; Cairncross, et al., 1995; Chen, et. al., 1995; Cairncross, et. al., 2000; Baer, et. al., 2000; Schunk and Rao, 1994; Bertram, et. al., 1998; Schunk, et. al., 2002).

Since the original publication of the GOMA 2.0 manual (see Schunk, et. al., 1998) work has further focused on concentrated chemical species transport (neutral and charged species) and Eulerian front tracking schemes for large material deformation problems. As in all other developments, these capabilities are being implemented in a fully-coupled way using Newton’s method. A concerted effort to bring these capabilities to bear on real-life problems has led to the addition of many esoteric features that address capillary wetting, phase change, charge neutrality, multicomponent species transport, and a host of other physical features. The best way to survey the available features is to consult the large library of reports, technical memoranda, tutorials, and other advanced feature manuals (e.g. Gates, et. al., 2000; Schunk, et. al., 1998; Rao, et. al., 2001; see Goma Documentation List in the Appendix), most of which are linked together with this manual in the CD version of the Goma Document System currently under development.

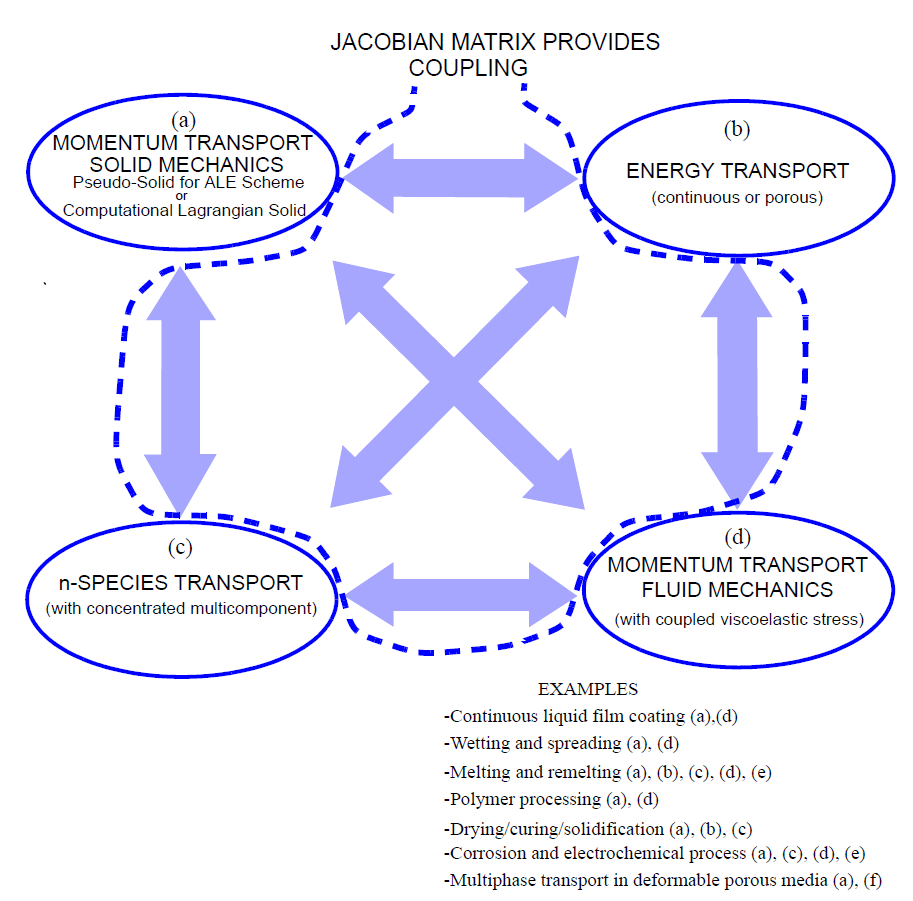
Main physics modules of Goma, their coupling and examples of potential applications.

Most recent developments, from 2006 through 2012, that are noteworthy are an extensive library of thin-shell physics/equations and accompanying boundary conditions, triangle and tetrahedral elements, phase-field modeling, parallel processing improvements and more. On the thin shell equations, the capability is fully coupled with continuum element equations. We have implemented theory and equations for Reynold’s lubrication (laminar or turbulent), thin-shell energy, thin-porous media, and surface rheology.

The purpose of this report is to provide a practical introduction and reference to Goma; to introduce the user to the range of options available in Goma; to show how easily the code may be adapted to investigate novel situations; and to provide a link to several simple illustrative examples as a tutorial and as a demonstration of the overall utility of the program. By design this is a reference manual which is best navigated together with a tutorial on the class of problems being addressed. It is recommended that perusal be undertaken section by section, consulting the individual input records as needed for a given problem.