Navier-Stokes Source#
Navier-Stokes Source = {model_name} {float_list} [varies]
Description / Usage#
This required card is used to specify the model for the fluid momentum source term vector in the Navier-Stokes equations. Gravitational and buoyancy effects often enter through this card.
Definitions of the input parameters are as follows:
{model_name} |
Name of the fluid momentum source term model for the Navier-Stokes equations. The model name will be one of the following strings:
|
{float_list} |
One or more floating point numbers (<float1> through <floatn>); the specific number is determined by the selection for {model _name}. |
Choices for {model_name} and the accompanying parameter list are given below; additional user guidance can be found in the Technical Discussion section following the Examples.
CONSTANT <float1> <float2> <float3> |
For a constant source model where the body force [M/L2t2] for this material does not vary. The {float_list} contains three values to specify the three components of the body force vector, where:
Note this source term has units of force/volume or, equivalently, density times acceleration. This is not true of all source term models. |
USER <float1>… <floatn> |
For a user-defined model; the set of {float_list} parameters are those required by specifications in the function usr_momentum_source. |
BOUSS <float1> <float2> <float3> |
This option specifies a generalized Boussinesq source where the density is linearly dependent upon temperature and concentration (species). The individual components of the constant acceleration vector a0 are read from the three entries in the {float_list}:
Unlike the CONSTANT model the units for these vector components are (L/t2), that is, they are true acceleration values. See the technical discussion below for the other parameters needed for this model. |
BOUSSINESQ <float1> <float2> <float3> |
This model prescribes a body force source term that is very similar to the BOUSS option except that the hydrostatic component is eliminated. The individual components of the constant acceleration vector a0 are read from the three entries in the {float_list}:
|
BOUSS_JXB <float1> <float2> <float3> <float4> |
This source model option specifies a generalized Boussinesq source term, as above, but also including Lorentz (electromagnetic) forces. The constant acceleration vector a0 is again specified using the first three constants that appear in the {float_list}. The fourth constant of the list is a Lorentz scaling factor (lsf). It may be used to scale the Lorentz term; see the Technical Discussion for more information.
|
EHD_POLARIZATION <float1> |
This source model option can be used to add on a dielectrophoretic force to the Navier-Stokes equations of the form ρE • ∇E ., where E is the electric field vector and ρ is a user-supplied constant with dimensions [q2T2/ L3]. This term requires the vector efield equation and the voltage equation to be solved simultaneously with the fluid-phase momentum equation. cf. EQ card definitions.
|
FILL <float1> <float2> <float3> |
This model prescribes the body force momentum source term for problems making use of volume-of-fluid interface tracking. The card prescribes a constant acceleration vector, usually the gravitational acceleration [L/T2]. It can only be employed when using the FILL density model. The individual components of the constant acceleration vector a0 are read from the three entries after the FILL string in the {float_list}, where:
|
LEVEL_SET <float1> <float2> <float3> |
This model prescribes the body force momentum source term for problems making use of level set interface tracking. The card prescribes a constant acceleration vector, usually the gravitational acceleration [L/T2]. It can only be used when also using the LEVEL_SET density model. The individual components of the constant acceleration vector a0 are read from the three entries after the LEVEL_SET string in the {float_list}, where:
|
PHASE_FUNCTION <float1> <float2> <float3> |
This model prescribes the body force momentum source term for problems making use of phase function interface tracking (a generalization of the level set method for more than two phases). The card prescribes a constant acceleration vector, usually the gravitational acceleration [L/T2]. It can only be used when also using the CONST_PHASE_FUNCTION density model. The individual components of the constant acceleration vector a0 are read from the three entries after the PHASE_FUNCTION string in the {float_list}, where:
|
VARIABLE_DENSITY <float1> <float2> <float3> |
This model sets the momentum body force source term for problems that employed the SOLVENT_POLYMER density model. The three parameters on the card are the individual components of a constant acceleration vector (usually due to gravity):
The actual body force applied is the local density computed from the SOLVENT_POLYMER model multiplied by this vector. |
SUSPEND <float1> <float2> <float3> <float4> |
This model prescribes a body force source term for suspensions where the carrier fluid and the particle phase have different densities. Four parameters must be set for this card using the {float_list}. The first three parameters (<float1>. <float2>, and <float3>) are the three components of the gravity vector. The fourth parameter (<float4>) is a reference concentration, Cref.
This source model requires a SUSPENSION density model be specified for the Density model. The density parameters on this card are used in this source model. If this momentum source term is used in conjunction with the HYDRODYNAMIC mass flux option, only one species can use the HYDRO diffusivity model. |
SUSPENSION <float1> <float2> <float3> <float4> |
This model is identical to the SUSPEND momentum source model (above), with the addition of mass source terms in the continuity equation due to transport of species with different densities.
This source model requires a SUSPENSION density model be specified for the Density model. The density parameters in this card are used in this source model. If this momentum source term is used in conjunction with the HYDRODYNAMIC mass flux option, only one species can use the HYDRO diffusivity model. |
ACOUSTIC <float1> <float2> <float3> <float4> |
This model includes the gradient of the acoustic Reynolds stress as a momentum source in addition to the usual gravitational source terms. The {float_list} contains four values to specify the three components of the body force vector plus a Reynolds stress gradient multiplier, where:
|
WARNING: Make sure the equation term multipliers for the source terms are set to unity.
Examples#
Following are some sample input cards:
Navier-Stokes Source = BOUSS 0. -980. 0.
Navier-Stokes Source = LEVEL_SET 0. -980. 0.
Technical Discussion#
This section contains user guidance, and theoretical background when appropriate, for each of the options for Navier-Stokes Source models.
CONSTANT |
A constant source model has a body force [M/L2t2] for the material which does not vary. A common usage of this model is for an incompressible fluid in a uniform gravitational field. Note that the source term has units of force/volume or, equivalently, density times acceleration. Thus, the values in the {float_list} would need to be specified as the product of the fluid density and the acceleration of gravity. |
USER |
This model option provides a means for the user to create a custom Navier-Stokes Source model for his/her special problem. The parameters of the model will be used by the source term model defined in the usr_momentum_source function. The {float_list} parameters are passed to this function as a one dimensional array named param in the order in which they appear on the card. The model must return a body force (force/volume) vector. An example use of this specification might be to construct a Coriolis acceleration term for a fluid in a rotating reference frame. |
BOUSS |
A generalized Boussinesq source term has the form where the linear dependence of the density upon temperature and concentration is used for this source term only. Density is assumed constant wherever else it happens to appear in the governing conservation equations. The density has been expanded in a Taylor series to first order about a reference state that is chosen so that, at the reference temperature T0 and concentration C0 the density is ρ0. The reference density is taken from the CONSTANT density model specified earlier in the material file on the Density card. The coefficient of thermal expansion of the fluid, β, is taken from the Volume Expansion card specified under Thermal Properties for this material. βc, is taken from the Species Volume Expansion card specified under species Properties for this material. The individual components of the constant acceleration vector a0 are the three entries of the {float_list} after the BOUSS string. Note that this BOUSS form includes the body force of the reference state so that a motionless fluid at a uniform temperature of T0 must be sustained by a linearly varying pressure field. Below, an alternative means for solving Boussinesq problems is presented that eliminates the constant hydrostatic feature of the BOUSS formulation. T0 is set on the Reference Temperature card. |
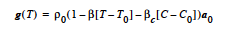
BOUSSINESQ |
This model prescribes a body force source term that is very similar to the BOUSS option except that the hydrostatic component is eliminated. Thus the form so that a no-flow solution with uniform temperature and concentration may be maintained by a constant pressure field. This form for the Boussinesq equations can sometimes provide a more well-conditioned equation system for weakly buoyant flows. Note again the implied convention that the coefficient of thermal expansion is positive when the density decreases with increasing temperature. That is, The same convention holds for the coefficient of solutal expansion. A source of confusion with buoyancy problems is that many sign conventions are applied. In addition to the convention for β, another possible source of confusion arises from a negative sign on the gravitational acceleration vector in many coordinate systems. That is, is a frequent choice for the constant acceleration for a twodimensional problem posed in Cartesian coordinates.T0 is set on the Reference Temperature card. |
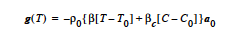
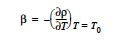
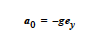
BOUSS_JXB |
This model is a generalized Boussinesq source term, as above, but also includes Lorentz forces. That is, the source term has the form where, in addition to the term defined for the BOUSS option, there is an added term due to electromagnetic forces acting upon a conducting fluid. The constant acceleration vector a0 is again specified using the first three constants that appear in the {float_list}. The fourth constant, lsf, may be used to scale the Lorentz term as desired (for example, lsf = 1 using a Gaussian system of units, or lsf = 1/c using a rationalized MKSA system of units). The two vector fields J, the current flux, and B, the magnetic induction, must be supplied to Goma in order to activate this option. At present, these fields must be supplied with the External Field cards, which provide the specific names of nodal variable fields in the EXODUS II files from which the fields are read. The three components of the J field must be called JX_REAL, JY_REAL, and JZ_REAL. Likewise the B field components must be called BX_REAL, BY_REAL, and BZ_REAL. These names are the default names coming from the electromagnetics code TORO II (Gartling, 1996). Because of the different coordinate convention when using cylindrical components, the fields have been made compatible with those arising from TORO II. It is the interface with TORO that also makes the Lorentz scaling (lsf) necessary so that the fixed set of units in TORO (MKS) can be adjusted to the userselected units in Goma. T0 is set on the Reference Temperature card. |
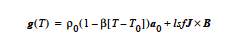
FILL |
The body force applied when using this momentum source model is as follows: where ρ1 and ρ0 are the phase densities obtained from the FILL density card, F is the value of the fill color function and the constant acceleration vector a0 is read from the three entries in the {float_list} of the FILL momentum source card. |
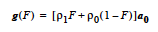
LEVEL_SET |
The body force applied when this model is used is given by the following function of the level set function value, φ: where is a smooth Heaviside function, φ is the value of the level set function, ρ+ and ρ- are the positive and negative phase densities, and α is the density transition length scale. The latter three parameters are obtained from the LEVEL_SET density card. The individual components of the constant acceleration vector a0 are three float parameters appearing in the {float_list} following the LEVEL_SET model name. |
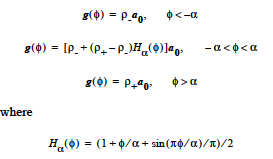
PHASE_FUNCTION |
The body force applied when this model is specified is identical in concept to that applied with the above LEVEL_SET model. The parameters on this card are simply the components of a constant acceleration vector (gravity in most applications). This card must be used in conjunction with the CONST_PHASE_FUNCTION density model because the actual body force vector is obtained by multiplying the acceleration vector specified with this card by the density computed by that latter model. Again this is identical in concept to the LEVEL_SET body force source model. |
SUSPEND |
This model prescribes a body force source term that is for simulating suspensions when the suspending fluid and particle phase have different densities. The difference in density can lead to buoyancy driven flow. The form of the source term is given below: where Ci is the solid particle volume fraction tracked using a species equation with a HYDRO diffusion model. Four parameters must be set for this card using the {float_list}. The first three parameters are the three components of the gravity vector. The fourth parameter is a reference concentration, Cref. The density values are those entered by a SUSPENSION density model on the Density card. NOTE: If this momentum source term is used in conjunction with the HYDRODYNAMIC mass flux option, only one species can use the HYDRO diffusivity model. |
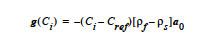
SUSPENSION |
This model is identical to the SUSPEND momentum source model in terms of the assembly of the momentum equation. However, this model creates a source term that gets applied during the assembly of the continuity equation due to transport of species with different densities. The suspension density models meet the definition of a locally variable density model, so the Lagrangian derivative of their densities can be represented as a divergence of mass flux. This term is integrated by parts and this particle phase flux is included separately as a source term for the continuity equation. |
ACOUSTIC |
This model contains the usual gravitational source terms in the CONSTANT model plus the gradient of the acoustic Reynolds stress as an additional momentum source. The acous_reyn_stress equation must be present to use this source model. |
The user should take special note of the distinction between the different use of the {float_list} for CONSTANT body force problems and for the various buoyant options. For the CONSTANT model, the three components are the force per unit volume, and the user must remember to include density specifically if it is desired. For the buoyancy options, the three components are acceleration, and the density value specified on a previous card is automatically used by Goma to construct the overall body force source term. This is also true for the FILL, LEVEL_SET, SUSPENSION and SUSPEND momentum source models.
The user must also take special care that the source term multipliers for the momentum equation are set to unity.
References#
Gartling, D. K., TORO II - A Finite Element Computer Program for Nonlinear Quasi- Static Problems in Electromagnetics, Part I - Theoretical Background, SAND95-2472, Sandia National Laboratories, Albuquerque, NM, May 1996.
