Capillary Network Stress#

Capillary Network Stress = {model_name}

Description / Usage#

This card specifies the mechanism by which capillary stress and capillary pressure in the liquid phase of a partially saturated porous medium is transferred to the solid network. This model is active only when the porous_deform equation (see EQ card) is active, and the drained network is deformable under liquid phase pressure. The principles of this card rest in the theory of the effective stress principle. In effect, the model specified here can be used to change the affinity of the pore liquid to the solid network (more discussion below). The input parameter is the model for capillary network stress.

The options for {model_name} are the names of transfer mechanisms:

WETTING

specifies that the porous skeleton has the same hydrostatic pressure as the liquid. This model has not been tested recently. See discussion below.

PARTIALLY_WETTING

specifies that the porous skeleton has a hydrostatic pressure that is the average of the liquid and gas phase pressures, weighted by their saturations (see related report on drying of deformable porous media by Cairncross, et. al., 1996).

COMPRESSIBLE

functions the same as the PARTIALLY_WETTING option but includes a factor that accounts for the compressibility of the solid material, viz. the actual struts of the solid material, not the network (see Cairncross, et. al., 1996).

Examples#

The following is a sample input card:

Capillary Network Stress = PARTIALLY_WETTING

Technical Discussion#

Basically, this card sets the functional form of the capillary stress contribution to the composite effective stress in a porous medium. The constitutive equation is as follows:

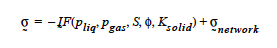
../../_images/408_goma_physics.png

where Ëśnetwork is the drained network stress that would result in the absence of any pore fluid (gas or liquid). The function F depends on the model type specified on this card. For POROUS_SATURATED media types, this card is not used and F = pliq. For POROUS_UNSATURATED and POROUS_TWO_PHASE media types, F is as follows for different transfer mechanisms:

  • WETTING: The assumption here is that a thin liquid layer covers all surfaces.

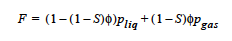
../../_images/409_goma_physics.png

  • PARTIALLY_WETTING: The most commonly used model.

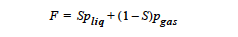
../../_images/410_goma_physics.png

  • COMPRESSIBLE: If the solid struts are also significantly compressible, viz. the solid bulk modulus Ks is of the same order of magnitude as the network skeleton bulk modulus, Kn, this model should be used. Not recently tested; please consult with Developers before using this option. PRS (6/13/2002)

References#

SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)