surf_charge#

EQ =surf_charge {Galerkin_wt} QS {Interpol_fnc} <float1> <float2> <float3>
<float4> <float5>

Description / Usage#

This card provides information for solving a conservation equation for the total surface charge in a 2-dimensional bar (or shell) element.. Note that this equation is not yet available in three dimensions and is in fact untested at this time. The card entries are as follows:

surf_charge

Name of the equation to be solved.

{Galerkin_wt}

Two- or four-character value that defines the type of weighting function for this equation, where:

  • Q1-Linear

  • Q2-Quadratic

QS

Name of the variable associated with the shell curvature equation.

{Interpol_fnc}

Two- or four-character value that defines the interpolation function used to represent the variable QS where:

  • Q1-Linear Continuous

  • Q2-Quadratic Continuous

<float1>

Multiplier for mass terms. Set to 1.0.

<float2>

Multiple for advection terms. Set to 1.0.

<float3>

Multiplier for boundary terms. Set to 1.0.

<float4>

Multiplier for diffusion terms - required but not currently implemented.

<float5>

Multiplier for source terms - required but not currently implemented.

Examples#

The following is a sample card that uses bilinear surface charge interpolation and weight function:

EQ = surf_charge Q2 QS Q2 1.0 1.0 1.0 0.0 0.0

Technical Discussion#

The surface charge conservation equation implemented is:

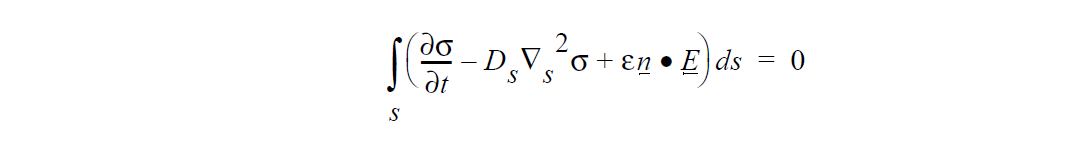
../../_images/302_goma_physics.png

where \(\sigma\) is the surface charge unknown, \(D_s\) is the surface diffusion coefficient, e is the electrical permittivity, \(\underline{n}\) is the unit normal vector to the surface, and \(\underline{E}\) = –\(\Delta\) V is the electric field vector. Here, advection contributions are not considered.

This is a special type of shell equation which depends on the gradient of a bulk variable (here, electric potential V). Since values of these variables away from the surface are normally not accessible during assembly of shell equations, this term has to be applied as a special type of boundary condition (WEAK_SHELL_GRAD) which is set up to evaluate sensitivities to interior bulk variable degrees of freedom . This term, though physically an integral part of the surface charge equation, is applied through the SURFACE_ELECTRIC_FIELD_BC boundary condition.

References#

Notz, Patrick K. Ph.D. thesis. Purdue University, 2000.