Category 8: Porous Equations#
The following conditions are applied as boundary conditions to the porous-flow equations. These conditions include strong Dirichlet conditions, such as hard sets on porous phase pressure on a boundary as a constant or function of position, weak-form conditions, such as a specified phase flux from a convective mass transfer model or a constant flux, and a host of interfacial conditions for impregnation, etc. The porous flow equations are actually scalar equations that represent component mass balances. Specifically, there is one component mass balance for the liquid phase, one for the gas phase, and one for the solid phase. The corresponding three dependent variables in these balances are the liquid phase pressure, the gas phase pressure, and the porosity, respectively. These variables are related to the flow through a boundary by their normal gradients (Darcy’s law formulation) and to the local inventory of liquid and gas through the saturation function. These implicit terms can often lead to some confusion in setting the boundary conditions so it is recommended that the user consult the supplementary documentation referenced in the following porous boundary condition cards.
POROUS_LIQ_PRESSURE#
BC = POROUS_LIQ_PRESSURE NS <bc_id> <float1> [float2]
Description / Usage#
(DC/POR_LIQ_PRES)
This Dirichlet boundary condition is used to set the liquid phase pore pressure at a noden set. It can be applied to a node set on a boundary of a POROUS_SATURATED, POROUS_UNSATURATED or POROUS_TWO_PHASE medium type (see Media Type card).
POROUS_LIQ_PRESSURE |
Boundary condition name (bc_name). |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of liquid phase pressure. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The boundary condition card
BC = POROUS_LIQ_PRESSURE NS 101 {pcmin}
sets the porous liquid pressure at the boundary denoted by node set 101 to the value represented by the APREPRO variable {pcmin}.
Technical Discussion#
Setting the porous liquid pressure to a value cannot be done independently of the saturation as the two are related through the vapor pressure curve for simulations in partially saturated media (see Saturation model card). Keep in mind that when using this card in these situations, you are setting also the saturation level based on the capillary pressure, defined as \(p_{gas}\) - \(p_{liq}\) = \(p_c\) . The convention in Goma is that when the capillary pressure \(p_c\) is greater than zero, the saturation level is less than unity, viz. the medium is partially saturated. When \(p_c\) is less than zero, i.e., when the liquid phase pressure is greater than the gas phase pressure, then the medium is saturated (in this case the capillary pressure is poorly defined, though). Also, for Media Type options of POROUS_UNSATURATED, the ambient gas pressure is constant within the pore space and is set by the Porous Gas Constants card in the material file. This boundary condition, when setting the liquid phase pressure, must be used with consideration of these definitions.
For saturated media (viz. Media Type of POROUS_SATURATED), this discussion is not relevant. In this case, one must only consider the pressure level as it may effect the isotropic stress in poroelastic problems.
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
POROUS_LIQ_FLUX_CONST#
BC = POROUS_LIQ_FLUX_CONST SS <bc_id> <float1> [float2]
Description / Usage#
(WIC/POR_LIQ_PRES)
This boundary condition sets the flux of liquid-phase solvent to a constant value in the Galerkin finite element weak sense. Specifically, this flux is applied to a side set as a weak-integrated constant and will set the net flux of liquid phase solvent component (in both gas and liquid phases) to a specified value. It can be applied to material regions of Media Type POROUS_SATURATED, POROUS_UNSATURATED, and POROUS_TWO_PHASE (see Technical Discussion below).
Definitions of the input parameters are as follows:
POROUS_LIQ_FLUX_CONST |
Name of boundary condition (<bc_name>). |
SS |
Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. |
<float1> |
Value of the liquid-solvent total flux, in M/ \(L^2\) -t. |
[float2] |
This optional parameter is not applicable to this boundary condition type, even though it is parsed if present. This parameter is used for boundary conditions of the Dirichlet type. |
Examples#
The input card
BC = POROUS_LIQ_FLUX_CONST SS 102 200.0
sets the total liquid-solvent mass flux, in both gas and liquid phases, to 200.0 along the side set 102.
Technical Discussion#
This boundary condition is of the mathematical form:
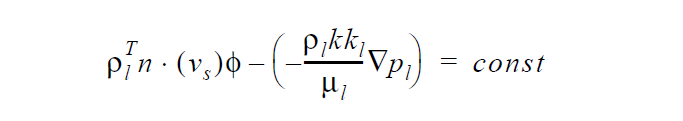
where \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card (this is usually zero except in advanced cases), \(p_l^T\) is the total bulk density of liquid phase solvent (in both gas and liquid phase, and hence depends on the local saturation), \(p_l\) is the pure liquid density, \(\phi\) is the porosity, \(p_l\) is the liquid phase pressure, and the other quantities on the second term help define the Darcy velocity. The const quantity is the input parameter identified above (<float1>). Note that this sets the flux relative to the boundary motion to the const value, but by virtue of the Galerkin weak form this condition is automatically applied with const =0 if no boundary condition is applied at the boundary. In a saturated case, viz. POROUS_SATURATED media type, this condition is applied as
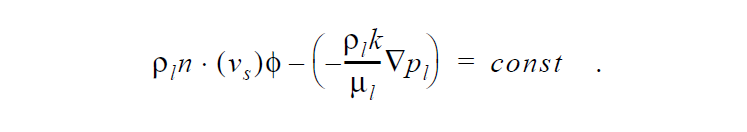
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
POROUS_GAS_PRESSURE#
BC = POROUS_GAS_PRESSURE NS <bc_id> <float1> [float2]
Description / Usage#
(DC/POR_GAS_PRES)
This Dirichlet boundary condition is used to set the gas-phase pore pressure at the boundary of a POROUS_TWO_PHASE medium type (see Media Type card). This condition makes no sense on other POROUS Media Types; the gas pressure in those cases is constant and set using the Porous Gas Constants card (Microstructure Properties).
POROUS_GAS_PRESSURE |
Boundary condition name (<bc_name>). |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float> |
Value of gas phase pressure. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The boundary condition card
BC = POROUS_GAS_PRESSURE NS 101 {pgas}
sets the porous gas pressure at the boundary denoted by node set 101 to the value represented by the APREPRO variable {pgas}.
Technical Discussion#
Setting the porous liquid pressure to a value cannot be done independently of the saturation as the two are related through the vapor pressure curve for simulations in partially saturated media (see Saturation model card). Keep in mind that when using this card in these situations, you are setting also the saturation level based on the capillary pressure, defined as \(p_{gas}\) - \(p_{liq}\) = \(p_c\) . The convention in Goma is that when the capillary pressure \(p_c\) is greater than zero, the saturation level is less than unity, viz.the medium is partially saturated. When \(p_c\) is less than zero, i.e., when the liquid phase pressure is greater than the gas phase pressure, then the medium is saturated (in this case the capillary pressure is poorly defined, though). Also, this pressure sets the datum of pressure for deformable porous media and must be set in a manner compatible with the solid-stress values on the boundaries of the porous matrix.
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
POROUS_GAS#
BC = POROUS_GAS SS <bc_id> <integer_list> <float_list>
Description / Usage#
(SIC/POR_LIQ_PRES)
This boundary condition card is used to equate flux of solvent in the porous medium and external gas. The condition is similar to the solid-liquid interface conditions that apply to interfaces between a porous medium and an external gas (in which the energy equation is used to solve for solvent concentration in the gas phase). This boundary condition is still in development.
There are three values in the <integer_list> and two values in the <float_list> for which to supply values; definitions of the input parameters are as follows:
POROUS_GAS |
Name of the boundary condition (<bc_name>). |
SS |
Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. |
<integer1> |
Element block ID of solid, porous phase from the EXODUS II database. |
<integer2> |
Element block ID of gas phase from the EXODUS II database. |
<integer3> |
Species number of liquid phase in porous medium. |
<float1> |
Vapor density. |
<float2> |
Factor to allow normal velocity in gas. |
Examples#
Users are referred to the Cairncross (1999) reference for the best example of card usage.
Technical Discussion#
This highly specialized boundary condition is best explained in a paper by Cairncross (1999).
References#
GTM-028.0: Modeling Drying of Dip-Coated Films with Strongly-Coupled Gas Phase Natural Convection, R. A. Cairncross, 1999.
POROUS_GAS_FLUX_CONST#
BC = POROUS_GAS_FLUX_CONST SS <bc_id> <float1> [float2]
Description / Usage#
(WIC/POR_GAS_PRES)
This boundary condition card is used to set the flux of gas-phase solvent to a constant value in the Galerkin finite element weak sense. Specifically, this flux is applied to a side set as a weak-integrated constant and will set the net flux of gas phase solvent component (in both gas and liquid phases, but because the gas solvent is assumed insoluble in the liquid phase, the liquid phase portion vanishes) to a specified value. This boundary condition can be applied to material regions of Media Type POROUS_TWO_PHASE only, as only this type contains a field of gas-phase solvent flux. (See technical discussion below).
Definitions of the input parameters are as follows:
POROUS_GAS_FLUX_CONST |
Name of the boundary condition (<bc_name>). |
SS |
Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. |
<float1> |
Value of the gas-solvent total flux, in M/ \(L^2\) -t. |
[float2] |
This optional parameter is not applicable to this boundary condition type, even though it is parsed if present. This parameter is used for boundary conditions of the Dirichlet type. |
Examples#
The input card
BC = POROUS_LIQ_FLUX_CONST SS 102 200.0
sets the total gas-solvent mass flux, in the gas phase only, to 200.0 along the side set 102.
Technical Discussion#
This boundary condition is of the mathematical form:
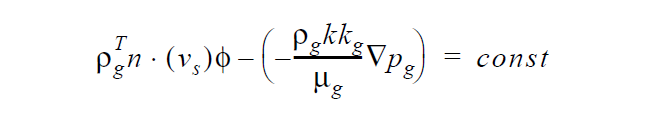
where \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card (this is usually zero except in advanced cases), \(p_g^T\) is the total bulk density of gas phase solvent (in both gas and liquid phase, and hence depends on the local saturation), \(p_g\) is the pure gas density, \(\phi\) is the porosity, \(p_g\) is the gas-phase pressure, and the other quantities on the second term help define the Darcy velocity. The const quantity is the input parameter described above (<float1>). Note that this sets the flux relative to the boundary motion to the const value, but by virtue of the Galerkin weak form this condition is automatically applied with const = 0 if no boundary condition is applied at the boundary.
POROUS_CONV#
BC = POROUS_CONV SS <bc_id> <integer>
Description / Usage#
(WIC/POR_LIQ_PRES)
This boundary condition is used to set the total flux of the liquid phase solvent (in both the gas and liquid phase) at the surface of a POROUS_UNSATURATED or POROUS_TWO_PHASE medium to the net convection of solvent due to a superimposed convective Lagrangian velocity (see Media Type card and Convective Lagrangian Velocity card). The only input is an integer indicating which component of the liquid phase solvent is to be set (as of 11/2/01 this component selectability option is not available and as indicated below should be set to zero; this card has not been tested).
Definitions of the input parameters are as follows:
POROUS_CONV |
Name of the boundary condition (<bc_name>). |
SS |
Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. |
<integer> |
Species number of transported species. (currently only used for multicomponent species in the phases, which as of 11/2/01 is not active, so set to zero). |
Examples#
Following is a sample card:
BC = POROUS_CONV SS 12 0
that applies a convective flux to side set 12 for porous liquid phase species 0. This species number is currently not used and ignored.
Technical Discussion#
This boundary condition has the following form
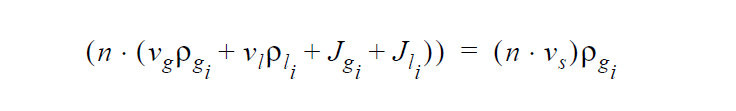
where the left hand side is the total flux of the solvent i in the medium, which includes, in order, the flux due to Darcy flow of gas vapor, the Darcy flow of liquid solvent, the diffusive flux of gas vapor in the pore space and the diffusive flux of liquid solvent in the liquid phase. \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card. As of now (11/2/01), this condition is used for a single component liquid solvent and has not been furbished for a single component of that solvent. Also, as of 11/02/01 the condition has not been tested.
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
POROUS_FLUX#
BC = POROUS_FLUX SS <bc_id> <integer> <float_list>
Description / Usage#
(WIC/POR_LIQ_PRES)
This boundary condition is used to set the total flux of the liquid phase solvent (in both the gas and liquid phase) at the surface of a POROUS_UNSATURATED or POROUS_TWO_PHASE medium to mass transfer coefficient times driving force (see Media Type card). The flux quantity is specified on a per mass basis so the mass transfer coefficient is in units of L/t, and the sink density is in units of M/ \(L^3\).
The <float_list> for this boundary condition has four values; the definitions of the input parameters are as follows:
POROUS_FLUX |
Name of the boundary condition (<bc_name>). |
SS |
Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. |
<integer> |
Species number of transported species (currently only used for multicomponent species in the phases, which as of 11/2/01 is not active; so set to zero). |
<float1> |
Value of mass transfer coefficient, \(h_1\) in units of L/t, consistent with gas phase concentration driving force. |
<float2> |
Driving force concentration in external phase, i.e., sink density, \(p_{gt}^0\) in units of M/ \(L^3\). |
<float3> |
Value of pressure-driven mass transfer coefficient, \(h_2\) in units of 1/L, for a liquid exiting a partially saturated domain. |
<float4> |
Driving force concentration in external phase, i.e., sink pressure for liquid extraction, \(p_{liq}^0\) in units of M/L/t. |
Examples#
Following is a sample card:
BC = POROUS_FLUX SS 12 0 0.03 0. 0. 0. 0.
This card applies the lumped mass transfer model for the liquid phase solvent with a mass transfer coefficient of 0.03 and a sink density of 0.0 for the total flux. The boundary condition is applied to side set 12 and to the species number 0. This species number is currently not used and ignored.
Technical Discussion#
The mathematical form for this boundary condition is as follows
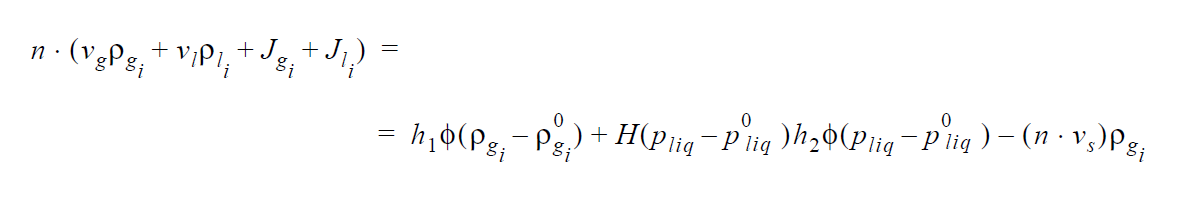
where the left hand side is the total flux of the liquid solvent i in the medium, which includes, in order, the flux due to Darcy flow of gas vapor, the Darcy flow of liquid solvent, the diffusive flux of gas vapor in the pore space and the diffusive flux of liquid solvent in the liquid phase. The parameters are \(h_1\), \(p_g^0\) , \(h_2\) , \(p{liq}^0\) and as defined on the input card. \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card.
At the present time (11/2/01), this condition is only used for single component liquid phases and has not been furbished for multicomponent capability yet. Note that usually the second term on the right is turned off, as in the example above, unless the liquid pressure at the surface of the sample is greater than the external pressure. This term was added for applications in which liquid is being squeezed out of a medium and then drips off or disappears, as liquid is not allowed to be sucked back in (Heaviside function, H), although the condition could be furbished for this.
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
POROUS_PRESSURE#
BC = POROUS_PRESSURE SS <bc_id> <integer1> <integer2>
Description / Usage#
(PCC/POR_LIQ_PRES)
This condition enforces a continuous fluid-phase pressure between material types, and is applied to a side set between two materials, one of type POROUS_SATURATED, POROUS_UNSATURATED, or POROUS_TWO_PHASE, and the other of type CONTINUOUS (see material card Media Type). Basically it sets the continuity of hydrodynamic pressure in the continuous fluid to the liquid Darcy pressure in the porous medium, at the interface. The input data is as follows:
POROUS_PRESSURE |
Name of the boundary condition (<bc_name>). |
SS |
Type of boundary condition (<bc_type>), where NS denotes side set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<integer1> |
Element block ID of the porous phase medium. |
<integer2> |
Element block ID of the continuous fluid phase medium. |
Examples#
An example input card for this boundary condition follows:
BC = POROUS_PRESSURE NS 101 1 2
This card sets the Darcy liquid phase pressure (p_liq in the output EXODUS II file) in element block 1 equal to the continuous phase hydrodynamic pressure (P in the output EXODUS II file) in element block 2.
Technical Discussion#
The mathematical form for this boundary condition is as follows
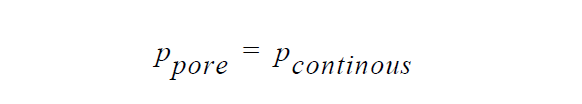
but its implementation is not; a memo describing the details of this boundary condition and how it is applied is cited below. This continuity of pressure is critical for the sensitivity of pressurizing the continuos phase to the penetration rate of the porous phase. Interestingly, it forces one to set the pore-phase pressure datum to the same datum in the continuous phase, and that effects the level of the Saturation versus capillary pressure curve (see Saturation material card).
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
P_LIQ_USER#
BC = P_LIQ_USER SS <bc_id> <float_list>
Description / Usage#
(PCC/R_POR_LIQ_PRES)
This boundary condition card is used to call a routine for a user-defined liquid-phase pressure for porous flow problems at an external boundary of a material of one of the following media types: POROUS_SATURATED, POROUS_UNSATURATED, POROUS_TWO_PHASE.. Specification is made via the function p_liq_user_surf in file “user_bc.c.” Definitions of the input parameters are as follows:
P_LIQ_USER |
Name of the boundary condition (<bc_name>). |
SS |
Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. |
<float_list> |
A list of float values separated by spaces which will be passed to the user-defined subroutine so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function in file user_bc.c. |
Examples#
The following is a sample input card with two parameters passed to function tuser:
BC =P_LIQ_USER SS 100 273.13 100.0
Technical Discussion#
No Discussion.
References#
No References.
POROUS_TEMPERATURE#
BC = POROUS_TEMPERATURE NS <bc_id> <float1> [float2]
Description / Usage#
(DC/POR_TEMP)
This Dirichlet boundary condition is used to set the temperature for a nonisothermal porous media problem at a node set. It can be applied to a node set on a boundary of a POROUS_SATURATED, POROUS_UNSATURATED or POROUS_TWO_PHASE medium type (see Media Type card).
POROUS_TEMPERATURE |
Boundary condition name (bc_name). |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of temperature at the NS in the porous medium. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
An example input card for this boundary condition follows:
BC = POROUS_TEMPERATURE NS 101 1.0 1.0
This card sets the temperature(p_temp in the output EXODUS II file) in element block 1 at the nodes defined by nodeset 101. Also, the second 1.0 float is to instruct goma to apply this condition in a residual form.
Technical Discussion#
This condition is used to set a temperature boundary condition for nonisothermal porous media problems, viz. problems that use the R_POR_ENERGY equation (called EQ = porous_energy). This energy equation is written in multiphase enthalpy form and hence requires a different equatioin that for continuous media.
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
