shell_deltah#
EQ = shell_deltah {Galerkin_wt} SH_DH {Interpol_fnc} <floatlist>
Description / Usage#
This card provides the capability to solve an evolution equation for a changing lubrication gap. The most common example of this would be a melting slider, as in the substrate of a snow ski or during high-energy sliding contact. Melting would change the lubrication gap. The Galerkin weight and the interpolation function must be set the same for the code to work properly. This equation could be furbished or advanced to handle other moving boundary problems which would lead to a changing gap. It should be noted, that gap changes due to a bounding flexible solid structure are already accommodated and fully compatible with this condition.
shell_deltah |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SH_DH |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SH_DH, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the source term. |
Examples#
Following is a sample card:
EQ = shell_deltah Q1 SH_DH Q1 1.0 1.0
This applies the equation with all terms activated.
Technical Discussion#
The equation solved is as follows:
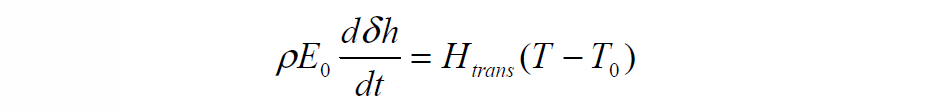
where \(E_0\) is the enthalpy, including the effect of phase change through the latent heat material property specified in the material file. \(H_{trans}\) is a heat transfer coefficient and is set in the material file as that due to melting/sliding contact (see material file section on MELTING_CONTACT). dh is the unknown.
The mass matrix multiplier activates the time-derivative term.
The source matrix multiplier activates the remaining term.
This equation is required to couple with SH_TEMP to solve for the local temperature. f
