Plastic Viscosity#

Plastic Viscosity = {CONSTANT | LINEAR} <float1> [float2] [M/L-t]

Description / Usage#

This card is used to specify the characteristic viscosity of plastic deformation and is required when the Plasticity Equation card is present. Definitions of the input model options are as follows:

CONSTANT

Name of the model for a constant plastic viscosity.

  • <float1> - the value of the viscosity.

LINEAR

LINEAR Name of the model for a linear variation in plastic viscosity; this model requires two floating point values as parameters.

  • <float1> - \(y_1\), the lower limit of plastic viscosity

  • <float2> - \(y_2\), the upper limit of plastic viscosity

Examples#

Following is a sample card:

Plastic Viscosity = LINEAR 1.0 100.

This specification results in a linear variation of plastic viscosity of the elastoviscoplasticity constitutive equation with concentration of solvent species according to the equation above.

Technical Discussion#

Using the concentration of solvent species as the independent variable in the LINEAR model, the viscosity y at a certain concentration c is:

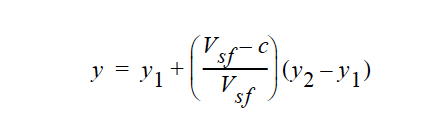
../../_images/373_goma_physics.png

where \(V_{sf}\) is the stress-free solvent volume fraction and the solvent volume fraction at solidification, which is set by the Stress Free Solvent Vol Fraction card in the material file. The input parameters for the LINEAR model are the plastic viscosity limits \(y_1\) and \(y_2\). NOTE: this model activates a linear dependence on concentration and hence can only be used for cases in which there is solvent transport.

So for a typical drying/solidification problem, the material file input deck requirements are shown as follows:

Stress Free Solvent Vol Frac = CONSTANT 0.6

Plasticity Equation = EVP_HYPER

Plastic Viscosity = LINEAR 1.0 2.0

EVP Yield Stress = CONSTANT 50.0

Together with these properties one must specify the elastic constants Lame Mu and Lame Lambda.

Theory#

See Schunk, et. al., 2001 (GT-019.1).

References#

GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001

GTM-020.0: In-Situ Characterization of Stress Development in Gelatin Film During Controlled Drying, M. Lu, S-Y Tam, P. R. Schunk and C. J. Brinker, March 2000.

GTM-027.0: Probing Plastic Deformation in Gelatin Films during Drying, M. Lu, S. Y. Tam, A. Sun, P. R. Schunk and C. J. Brinker, 2000.

S.Y. Tam’s thesis: “Stress Effects in Drying Coatings,” Ph.D Dissertation, University of Minnesota, 1997