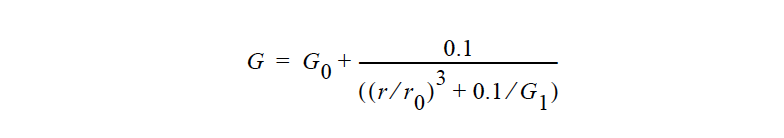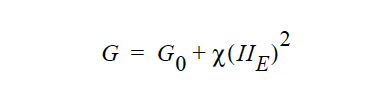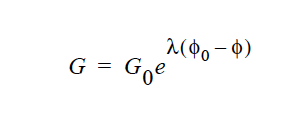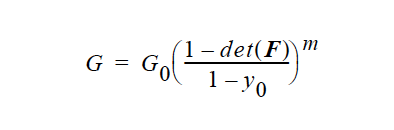Lame MU#
Lame MU = {model_name} {float_list} [M/ :math:`Lt^2`]
Description / Usage#
This required card is used to specify the model for the Lame coefficient μ for the solid constitutive equation (see Sackinger, et. al. 1995, and Solid Constitutive Equation card); this coefficient is equivalent to the shear modulus G in most cases, as described below.
Definitions of the input parameters are as follows:
{model_name} |
Name of the Lame Mu coefficient model. This parameter can have one of the following values: CONSTANT, POWER_LAW, CONTACT_LINE, SHEAR_HARDEN, EXPONENTIAL, DENSE_POWER_LAW, or USER. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model. |
The details of each model option are given below:
CONSTANT <float1> |
For the CONSTANT model, {float_list} is a single value: <float1> - Standard value of the coefficient \(\mu\). (See Technical Discussion.) |
POWER_LAW <float1> <float2> <float3> |
The POWER_LAW model is only to be used for deformable porous media where the shear modulus is allowed to vary as a power of the porosity, \(\phi\) (see Scherer, 1992): The {float_list} contains three values for this model, where: .. figure:: /figures/360_goma_physics.png :align: center :width: 90%
|
CONTACT_LINE <float1> <float2> <float3> <float4> |
The CONTACT_LINE model is a convenient way to control mesh deformation near a fixed point and is normally used ONLY for ARBITRARY Mesh Motion types. This model enables the user to make the shear modulus much larger near the contact line (fixed point) than far away from the contact line, so that elements near the contact line are forced to retain their shape. The shear modulus in this model varies inversely with distance from the contact line: 
r is the distance from the fixed point, \(r_0\) is a decay length, \(G_0`is the modulus far from the contact line, and :math:`G_0 + G_1\) is the modulus at the contact line. The {float_list} contains four values for this model, where:
|
SHEAR_HARDEN <float1> <float2> |
The SHEAR_HARDEN model is: 
where \(\chi\) is the coefficient of variation, \(II_E\) is the second invariant of the strain tensor (see Solid Constitutive Equation card), \(G_0\) is the modulus at zero shear. The {float_list} contains two values for this model, where:
|
EXPONENTIAL <float1> <float2> <float3> |
The EXPONENTIAL model is used exclusively for poroelastic problems, and allows for an exponential dependence of the shear modulus \(\mu\) (or G) on porosity: 
where \(\lambda\) is the rate of decay, \(\phi_0\) is the porosity in the stress-free state, \(G_0\) is the modulus at zero shear.
|
DENSE_POWER_LAW <float1> <float2> |
The DENSE_POWER_LAW model is used mostly for drying/consolidation problems for which it is desired to have a plateau max-pack modulus behavior. This option requires input from the Stress Free Solvent Vol Frac card (\(y_0\) in equation below), and is used for solvent drying from a condensed, gelled phase. The functional form for the shear modulus is 
where m is the power law exponent, F is deformation gradient tensor (see Solid Constitutive Equation card), and \(G_0\) is the modulus at zero shear. This function is truncated or clipped at the low end value at G=:math:10^-12.
|
TABLE <integer1> <character_string1> {LINEAR | BILINEAR} [integer2] |
Please see discussion at the beginning of the material properties chapter 5 for input description and options. |
USER <float1>,…, <floatn> |
For the USER model, {float_list} is of arbitrary length, and the values are used through the param[] array in usr_lame_mu function to parameterize a user-defined model. See examples in user_mp.c. |
All modulus values in these equations have the same units as Lame Mu, i.e., M/Lt2.
Examples#
The following is a sample card:
Lame MU = CONSTANT 1.
Technical Discussion#
Note that \(\mu\) and \(\lambda\), (see the Lame LAMBDA card) are related to the more often used Young’s Modulus and Poisson’s Ratio by the following standard expressions:
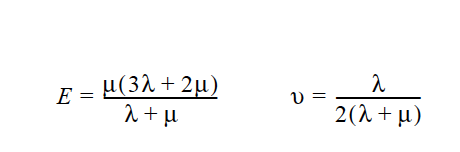
where E is the Young’s modulus and υ is Poisson’s ratio. A significant limiting case is approached as \(\nu\) approaches 0.5, in which case the solid becomes incompressible.
The POWER_LAW option could easily be adapted to a concentration measure, viz. made dependent on the concentration of some species (see EQ = species_bulk card). This can be done through the user option, and in fact in usr_lame_mu function of file user_mp.c in the Goma distribution has an example that is appropriate. Also note that all of these models are available for the elastoviscoplastic option on the Plasticity card, and for the real-solid in TOTAL_ALE mesh motion.
FAQs#
Important note that when one desires an incompressible solid through the use of INCOMP_PSTRAIN type models, by using an incompressible continuity equation in a LAGRANGIAN mesh region (see EQ = continuity), then the bulk modulus, or Lame Lambda expansion term is also added on. So to get a truly incompressible response, one must set the Lame LAMBDA coefficient to zero.
References#
Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.
Scherer, G.W., 1992, “Recent Progress in Drying of Gels”, J. of Non-Crystalline Solids, 147&148, 363-374
GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche
GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001
GTM-027: Probing Plastic Deformation in Gelatin Films during Drying, M. Lu, S. Y. Tam, A. Sun, P. R. Schunk and C. J. Brinker, 2000
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)