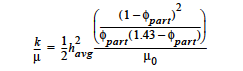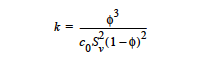Permeability

Permeability = {model_name} {float_list} [L2]

Description / Usage

This card is used to specify the model for permeability, which is required for the Brinkman and Darcy formulations for flow through porous media. Definitions of the input parameters are as follows:

{model_name}	Name of the permissible models for permeability: CONSTANT, TENSOR, KOZENY_CARMEN, SOLIDIFICATION and PSD_VOL, PSD_WEXP, or PSD_SEXP. (No USER model as of 6/13/2002; contact Developers for this addition).
{float_list}	One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}.

Permeability model choices and their parameters are discussed below.

CONSTANT <float1>	Model for constant permeability with a single parameter. This model is allowed for all Media Types (cf. Media Type card). <float1> - k, Permeability [L2]
TENSOR <float1> <float2> <float3> <float4>	Model for a two dimensional, constant anisotropic permeability; it has not been implemented in three dimensions. All media types (cf. Media Type card) except POROUS_BRINKMAN may use this model. <float1> - \(k_{xx}\) permeability [L2] <float2> - \(k_{yy}\) permeability [L2] <float3> - \(k_{xy}\) permeability [L2] <float4> - \(k_{yx}\) permeability [L2]
PSD_VOL <float1> <float2> <float3> <float4>	This is a model of a deformable medium with a probabilistic distribution of pore sizes; see Technical Discussion section. Four parameters are required for the PSD_VOL model: <float1> - φ0, porosity in undeformed state <float2> - rmax(φ0), maximum pore radius in undeformed state <float3> - α, ratio of smallest pore size to largest pore size <float4> - 1 ⁄ τ2, a geometric tortuosity factor All media types (cf. Media Type card) except POROUS_BRINKMAN may use this model
PSD_WEXP <float1> <float2> <float3> <float4>	Same <float> specifications as PSD_VOL model. This model is allowed for all media types except POROUS_BRINKMAN (cf. Media Type card).
PSD_SEXP <float1> <float2> <float3> <float4>	Same <float> specifications as PSD_VOL model. This model is allowed for all media types except POROUS_BRINKMAN (cf. Media Type card).
SOLIDIFICATION <float1>	Used to phase in a porous flow term in the liquid momentum equations for low volume fraction packing of particles in the Brinkman porous flow formulation (see discussion below). Used for Phillip’s model of suspensions for the Liquid Constitutive Equation, viz. CARREAU_SUSPENSION, SUSPENSION, FILLED_EPOXY or POWER_LAW_SUSPENSION. <float1> - the species number of the suspension flow model; it is used to indicate that maximum packing, or solidification has occurred. (The float is converted to an integer). This model is ONLY allowed for media type POROUS_BRINKMAN (cf. Media Type card). The functional form is: where μ0 is the clear fluid viscosity, φpart is the volume fraction of particles, or concentration divided by the maximum packing (0.68 for monodisperse spheres), and havg is the average element size.
KOZENY_CARMAN <float1> <float2>	The Kozeny-Carman equation relates the permeability to the porosity for a porous medium and has been shown to fit well the experimental results in many cases. This. equation is easily derivable from the PSD_* models for the case of uniform pore-size distribution, viz. a delta distribution (cf. Cairncross, et. al., 1996 for derivation). The model is currently implemented in the isotropic media case and is useful for deformable problems in which the porosity changes with deformation (cf. Porosity card DEFORM model). The functional form for this model is as follows: Here φ is the porosity, c0 is a constant consisting of tortuosity and shape factor of the pores, and Sv is the surface area per solid volume. The float parameters are: <float1> - c0 , tortuosity and shape factor <float2> - Sv , surface area per solid volume
EXTERNAL_FIELD <float1>	This model reads in an array of values for the porosity from an initial exodus file. This allows for spatial variations in the parameter value. <float1> - Scale factor for converting/scaling exodusII field. The ExodusII field variable name should be “PERM”, viz. External Field = PERM Q1 name.exoII (see this card)

Examples

Following is a sample card:

Permeability = CONSTANT 0.001

This specification leads to a constant permeability of 0.001.

Technical Discussion

For all models, this card provides the permeability, in units of [L2]. For saturated porous materials (viz. POROUS_BRINKMAN or POROUS_SATURATED media types), the viscosity from the Viscosity card is used to compute the porous conductivity, viz., permeability divided by viscosity. For unsaturated media types, the viscosity factor comes through the relative permeability cards (see Rel Gas Permeability and Rel Liq Permeability cards). Please consult the references below for the proper form of the equations.

The PSD_VOL (Probability Size Distribution, PSD) model treats the medium as a bundle of capillary tubes with a distribution of pores such that over a range of porek sizes the volume of pores is evenly distributed. For such a model, the maximum poresize varies with the porosity:

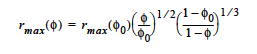
Then, the permeability is a function of the maximum pore-size and the pore-size distribution:

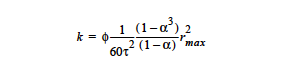
The input parameters for the PSD models are φ0, rmax(φ0), α, and 1 ⁄ τ2. More detail on the deformable porous medium models is given in Cairncross, et. al., 1996. The PSD_WEXP and PSD_SEXP are similar pore-size distribution models to PSD_VOL. The references below should be consulted for details on how to use these models.

References

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)