Species Source#

Species Source = {model_name} <species> <float_list> [varies]

Description / Usage#

This required card is used to specify the model for the source term on the species convection diffusion equations. Definitions of the input parameters are as follows:

{model_name}

Name of the model for the source term on the species convection diffusion equations. The permissible values are

CONSTANT

BUTLER_VOLMER

ELECTRODE_KINETICS

ELECTROOSMOTIC

EPOXY

EPOXY_DEA

FOAM

USER

An integer designating the species equation.

<float_list>

One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}.

Source-term model choices and their parameters are discussed below. Details are contained in the Technical Discussion section below. The <species> definition given above applies to all the following choices for which it is specified; its definition will not be repeated.

CONSTANT <species> <float1>	This model of a constant species source has a single input value: <float1>-Constant species source
BUTLER_VOLMER <species> <float1> <float2> <float3> <float4> <float5> <float6> <float7> <float8> <float9>	This is the homogeneous species source or sink term (in units of moles per unit volume, e.g. moles/cm3-s) as described by the Butler-Volmer kinetic model (see the Theory section below). One integer and 9 flotas are required: <species> - Index of the species involved in the electrochemical reaction (here, we assume that only a single species is involved). <float1> - Stoichiometric coefficient, s. <float2> - Product of interfacial area per unit volume by exchange current density, ai0, in units of A/cm3. <float3> - Reaction order, β. <float4> - Reference species concentration, cref, in units of moles/cm3. <float5> - Anodic transfer coefficient, αa. <float6> - Cathodic transfer coefficient, αc. <float7> - Temperature, T, in unit of K. <float8> - Open-circuit potential, U0, in unit of V. <float9> - Number of electrons involved in the reaction, n.
ELECTRODE_KINETICS	The ELECTRODE_KINETICS model is used to specify the species generation or consumption in electrochemical processes involving concentrated electrolyte solutions and multiple species such as thermal batteries. The {model_name} ELECTRODE_KINETICS toggles on the option in the equation assembly; no parameters are required.
ELECTROOSMOTIC <int1> <int2> <float1> <float2> <float3> <float4> <float5> <float6> <float7> <float8> <float9> <float10>	This is the source or sink term (in units of moles per unit volume, e.g. moles/cm3-s) for thw water species due to electro-osmotic drag by the protons (H+). Two integers and 10 flotas are required: <int1> - Water species index. <int2> - Index of the species involved in the electrochemical reaction that generates the electrical current (here, we assume that only a single species is involved). <float1> - Stoichiometric coefficient, s. <float2> - Product of interfacial area per unit volume by exchange current density, ai0, in units of A/cm3. <float3> - Reaction order, β. <float4> - Reference species concentration, cref, in units of moles/cm3. <float5> - Anodic transfer coefficient, αa. <float6> - Cathodic transfer coefficient, αc. <float7> - Temperature, T, in unit of K. <float8> - Open-circuit potential, U0, in unit of V. <float9> - Number of electrons involved in the reaction, n. <float10> - Electro-osmotic drag coefficient, nd.
EPOXY <species> <floatlist>	The EPOXY model adds a reaction source term for a condensation polymerization reaction based on an extent of reaction variable. Six model parameters make up the <float_list> for the EPOXY species source model, as follows: <float1> - A1 (prefactor) <float2> - E1/R (activation energy/gas constant) <float3> - A2 (prefactor) <float4> - E2/R (activation energy/gas constant) <float5> - m (exponent) <float6> - n (exponent) This model will be used with the EPOXY Heat Source model to compute the reaction rate.
EPOXY_DEA <species> <floatlist>	The EPOXY_DEA model was created specifically for a diethanolamine-epoxy curing reaction, a different model of the reaction kinetics from the EPOXY source model. The <float_list> for EPOXY_DEA species source model has five values, where <float1> - A1 <float2> - E1/R <float3> - A2 for the low-temperature regime <float4> - E2/R for the low-temperature regime <float5> - A2 for the mid-temperature regime
FOAM	The FOAM model was created specifically for the removable epoxy foam decomposition kinetics. However, the basis for evolving the density change can be applied to other reactive material models. There are eight float inputs in <float_list> which are used to specify two Arrhenius-type reaction rates r1 and r2 and two reference temperatures T1 and T2: <float1> - A1 <float2> - E1 <float3> - sig_1 (not currently used). <float4> - A2 <float5> - E2 <float6> - A2 sig_2 (not currently used) <float7> - T1 <float8> - T2 where Aj and Ej are the Arrhenius pre-exponential factor and activation energy, respectively, for reaction rate rj, and T1 and T2 are used to define a dimensionless problem temperature T∗ = (T – T1) ⁄ (T2 – T ).
USER <species> <floatlist>	The USER option indicates that a user-defined model has been introduced into the usr_species_source routine in the user_mp.c file. The <float_list> is of arbitrary length subject to the user’s requirements to parameterize the model.

Examples#

Sample card for the CONSTANT model:

Species Source = CONSTANT 0 2.

Sample card for the BUTLER_VOLMER model:

Species Source = BUTLER_VOLMER 1 -1. .02 1. 4.e-5 1. 1. 353. 1.18 4.

Sample card for the ELECTROOSMOTIC model:

Species Source = ELECTROOSMOTIC 2 1 1. .02 1. 4.e-5 1. 1. 353. 1.18 4.0 1.4

Technical Discussion#

A discussion of units for species flux terms can be found under FAQs on the Diffusivity card.

The CONSTANT option offers the simplest way for prescribing a constant homogeneous rate of species generation or consumption involving in a speciestransport process.

In the BUTLER_VOLMER model, the current source or sink due to a homogeneuous electrochemical reaction involving a single species (e.g., the hydrogen oxidation and oxygen reduction reactions in a hydrogen-feuled polymer-electrolyte-membrane fuel cell) is computed using the Butler-Volmer kinetic model as described below in the Theory section.

The ELECTRODE_KINETIC model computes the molar rate of electrolyte-species generation or consumption in electrochemical processes involving concentrated electrolyte solutions and multiple species as in thermal batteries. The molar rate of electrolyte-species consumption is evaluated using Butler-Volmer kinetics along with Faraday’s law. Further details can be found in the reference listed below in the References sub-section (Chen et al. 2000).

The ELECTROOSMOTIC model computes the water-species flux due to the electroosmotic drag of protons (H+), which is proportional to the average current density with the proportionality constant being the electro-osmotic drag coefficient, nd.

The EPOXY model adds a reaction source term for a condensation polymerization reaction based on an extent of reaction variable. The extent of reaction is tracked as a convection equation with a reaction source term. The form of the EPOXY species source term is

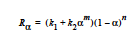
where α is the extent of reaction, the rate constants, k1 and k2, can depend on temperature in the Arrhenius manner, and m and n are exponents.

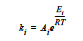
where R is the gas constant in the appropriate units, Ai is the prefactor, and Ei is the activation energy for reaction. Six parameters are required to define the model: A1 and A2 (prefactors), E1 and E2 (activation energies), and m and n (exponents), with R being the universal gas constant.

The EPOXY_DEA model was created specifically for diethanolamine-epoxy curing reaction. While the expression for the source term is identical to the EPOXY model (with n=1.6),

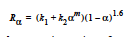
the reaction kinetics differs, having three reaction regimes for exponent m and rate constant k2. For T< 65 C, m = 2 and

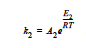
for 65 C < T< 90C, m = 74*k2 and

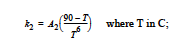
and for T > 90C, m = k2 = 0. Rate constant k1 is fixed for all these regimes and is determined from the prefactor A1 and activation energy E1.

The FOAM model computes the mixture volume change rate as:

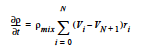
where ρmix is the mixture density as defined in the REACTIVE_FOAM density model (which is required for this model) and Vi is the specific volume of component i.

The USER option indicates that a user-defined model has been introduced into the usr_species_source routine in the user_mp.c file. The <float_list> is of arbitrary length subject to the user’s requirements to parameterize the model.

Theory#

The rate of species generation or consumption in electrochemical processes involving a single species such as polymer-electrolyte-membrane fuel cells can be computed using the Butler-Volmer kinetic model and the Faraday’s law (cf. Newman 1991, Chen et al. 2000, Chen and Hickner 2006):

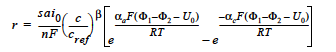
where r is the homogeneous species source or sink in units of moles/cm3-s; s is the stoichiometric coefficient with a sign comvention such that r represents a source when s > 0 and sink when s < 0; n is the number of electrons involved in the electrochemical reaction; ai0 denotes the product of interfacial area per unit volume by exchange current density, which has units of A/cm3; c and cref are, respectively, species and reference molar concentrations in units of moles/cm3; β is reaction order; αa and αc are, respetively, the anodic and cathodic transfer coefficients; F is the Faraday’s constant ( ≡ 96487 C/mole) and R is the universal gasl constant ( ≡ 8.314 J/mole-K); and are, respectively, the electrode and electrolyte potentials in unit of V; U0 is the open-circuit potential in unit of V; and T is temperature in unit of K.

References#

for EPOXY_DEA Model GTM-011.0: Validation of 828/DEA/GMB Encapsulant using GOMA, August 20, 1999, A. C. Sun

for BUTLER_VOLMER and ELECTRODE_KINETIC Models:

J. Newman, Electrochemical Systems, 2nd Edition, Prentice-Hall, Englewood Cliff, NJ (1991).

K. S. Chen, G. H. Evans, R. S. Larson, D. R. Noble, and W. G. Houf, “Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions”, Sandia Report SAND2000-0207 (2000).

K. S. Chen and M. A. Hickner, “Modeling PEM fuel cell performance using the finiteelement method and a fully-coupled implicit solution scheme via Newton’s technique”, in ASME Proceedings of FUELCELL2006-97032 (2006).