Diffusion Constitutive Equation#
Diffusion Constitutive Equation = {model_name}
Description / Usage#
This card is used to specify the constitutive equation governing mass transport. Definitions of the input parameters are as follows:
{model_name} |
Name of the model for the diffusion constitutive equation. The currently supported options are:
|
This card requires only the specification of a {model_name}. The Technical Discussion subsection below presents each of these models.
Examples#
The following is a sample input card:
Diffusion Constitutive Equation = DARCY
Technical Discussion#
NONE indicates that the material block to which this material file applies is a nondiffusing material. FICKIAN implies that the rate of diffusion is proportional to the gradient in volume fraction and the diffusion coefficient of each species. DARCY implies that mass transport occurs by pressure-driven flow through a porous medium. DARCY_FICKIAN implies that mass transport occurs by both diffusion and pressuredriven flow in a porous medium.
HYDRODYNAMIC implies that mass transport of at least one species is driven by gradients in the second invariant of the rate of deformation tensor (shear rate) and gradients in viscosity (Phillips, et.al. 1992). This model also includes a sedimentation flux term to account for the motion of non-neutrally buoyant particles resulting from gravitation (Zhang and Acrivos, 1994) and a curvature-driven flux term from the normal component of the acceleration vector (Krishnan et al., 1996). This model is used in predicting the particle distributions of particulate suspensions undergoing flow. For this model, the mass flux vector J is given by the following:
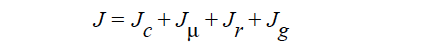
where
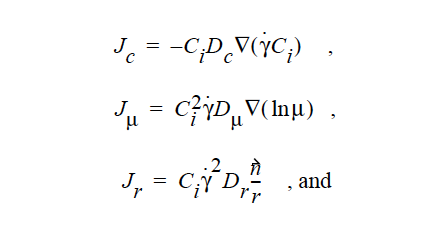
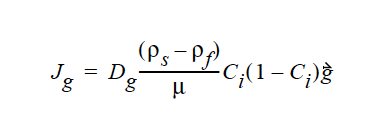
where Ci is the particulate phase volume fraction, i is the species number designation of the particulate phase, the shear rate, μ the viscosity, the normal unit acceleration vector, r the curvature of streamlines, Dc, Dμ, Dr and Dg the “diffusivity” parameters, ρs and ρf the particle and fluid phase densities, respectively, and , the gravitational acceleration vector.
GENERALIZED_FICKIAN is based on the generalized-Fick’s law (Taylor and Krishna, 1993). The mass transport of each species is influenced by all of the species in the mixture.
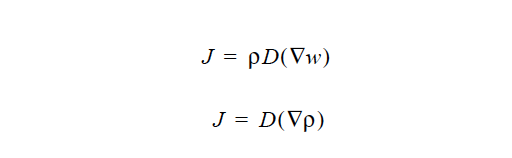
ρ is the mass-concentration of species. The elements along the diagonal, Dii, are selfdiffusivities, while Dij are mutual-diffusivities between species i and j. Note that mutual diffusivities in generalized formulation can be both positive and negative.
FICKIAN_CHARGED indicates a model for multicomponent transport (diffusion and migration) of charged species in dilute electrolyte solutions will be used. The Fickian diffusivity of species i, Di, as defined in the following Fickian flux model (cf. Newman 1991; Chen 2000)
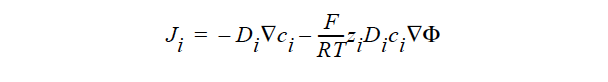
is taken to be constant. Here, ci is molar concentration of species i, Φ is electrical potential in electrolyte solution, zi is charge number of species i, F is the Faraday constant (96487 C/mole), R is the universal gas constant (8.314 J/mole-K), and T the electrolyte solution temperature.
STEFAN-MAXWELL activates a model for multicomponent diffusion of neutral species in concentrated solutions. The Stefan-Maxwell diffusivities, Dij, as defined in the following Stefan-Maxwell flux model (cf. Chen et al. 2000, Chen et al. 1998):
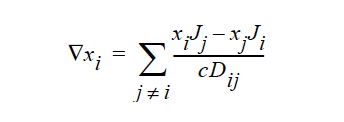
are taken to be constant. Here, xi is mole fraction of species i, Ji the molar flux of species i, and c the total molar concentration. Since Dij = Dji and Dii are not defined, only n(n-1)/2 Stefan-Maxwell diffusivities are required (here, n is the total number of diffusing species). For example, for n = 3 (i.e., a solution having three species), three Stefan-Maxwell diffusivities are needed: D12, D13, and D23.
STEFAN-MAXWELL_CHARGED For multicomponent transport (diffusion and migration) of charged species in concentrated electrolyte solutions. The Stefan- Maxwell diffusivities, Dij, as defined in the following Stefan-Maxwell flux model (cf. Chen et al. 2000, Chen et al. 1998)
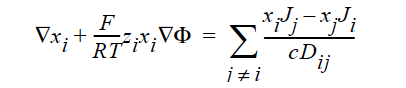
are taken to be constant, as in the case of multicomponent diffusion of neutral species in concentrated solutions. Here, the charged species definitions are the same as for the FICKIAN_CHARGED model.
References#
GTM-025.0: Chen, K. S., “Modeling diffusion and migration transport of charged species in dilute electrolyte solutions: GOMA implementation and sample computed predictions from a case study of electroplating”, Sandia memorandum, September 21, 2000.
Chen, K. S., Evans, G. H., Larson, R. S., Noble, D. R., and Houf, W. G. “Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions”, SAND2000- 0207, Sandia National Laboratories Technical Report (2000).
Chen, K. S., Evans, G. H., Larson, R. S., Coltrin, M. E., and Newman, J. “Multidimensional modeling of thermal batteries using the Stefan-Maxwell formulation and the finite-element method”, in Electrochemical Society Proceedings, Volume 98-15, p. 138-149 (1998).
Krishnan, G. P., S. Beimfohr, and D. Leighton, 1996. “Shear-induced radial segregation in bidisperse suspensions,” J. Fluid Mech. 321, 371
Newman, J. S., Electrochemical Systems, Prentice Hall, Inc., Englewood Cliffs, New Jersey (1991).
Phillips, R.J., R.C. Armstrong, and R.A. Brown, 1992, “A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration,” Physics of Fluids A, 4(1), 30-40.
Taylor, R. and R. Krishna. 1993. Multicomponent Mass Transfer. John Wiley & Sons, New York.
Zhang K., and A. Acrivos, 1994, “Viscous resuspension in fully-developed laminar pipe flows,” Int. J. Multiphase Flow, (20)3, 579-591.
