Liquid phase compressibility#
Permeability = {model_name} {float_list} [L2]
Description / Usage#
This card specifies the model and model parameters for liquid-phase compressibility, and was specifically designed for use in porous-media flow problems that are partially saturated (viz. Media Type card values of POROUS_UNSATURATED or POROUS_TWO_PHASE). This feature was added partially for numerical convenience in rigid porous media to accommodate regimes where the saturation level is at or near unity; at these saturation levels the capacitance term (see Technical Discussion below) all but vanishes, viz. there is no sensitivity of the saturation level to liquid phase pressure, and the mathematical behavior can change type. This occurs in situations of low permeability, narrow pore-size distribution, and sudden pressure spikes during simulation startup.
CONSTANT |
Name of the model for the compressibility coefficient, currently the only option. It requires a single parameter:
|
This card requires a companion card Liquid phase reference pressure.
Examples#
The cards (using APREPRO variables)
Liquid phase compressibility = CONSTANT {beta_liquid}
Liquid phase reference pressure = CONSTANT {p_not}
leads to the application of a linearized compressibility model for the density of liquid in the time-derivative capacitance term. This is useful for rigid porous media when the conditions are such that the saturation front is sharp.
Technical Discussion#
For Cls the most part, we have needed the Liquid Phase Compressibility capability to ease the startup of impregnation problems, in which an external pressure load is impulsively applied to a liquid layer being forced into a rigid porous matrix. The capacitance term as the saturation level approaches 1.0 (S->1) in the porous Darcy flow equation appears in Goma as
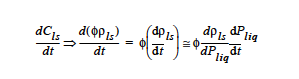
Here is the liquid solvent concentration (in both gas and liquid phases), φ is the porosity, ρls and is the liquid phase density. Here we employ the linearized density model:
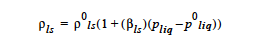
where βls is the coefficient of compressibility entered on this card, viz. dρls ⁄ dPliq defined above, p0liq is the reference liquid pressure (see Liquid phase reference pressure* card)
FAQs#
The following troubleshooting tips regarding startup of partially saturated porous media problems are part of the authors experience presented in Schunk, 2002 (GT- 009.3):
-Linear elements, viz. Q1 elements, are better for saturation front startup at an external boundary if the difference between the boundary specified liquid-phase pressure and the medium-initialized liquid phase pressure are drastically different. Quadratic elements in this case can lead to zero or low Saturation values at all computational Gaussian integration points and the front may never penetrate.
-Time stepping is all important. There are three relevant parameters: time-step scheme, initial time step size, and time-step error factor. The rules of thumb that can be established are as follows:
If you are using Porous Mass Lumping, you must set the Time Step Parameter to 0.0, or your performance will suffer. In fact, it is always a good idea in steep penetration front problems to use backward Euler techniques.
With mass lumping and first order time integration, you must control your step size with the tolerance setting. Too big of time step early on can propagate to large errors at later times when time stepping. You may need to experiment with the error tolerance on the Time step error card. Constantly scrutinize your results for correctness and suspect an error growth here.
You must have a significant capacitance term on the first time step. If your capacitance term is small, then the problem is elliptic and will try to satisfy all boundary conditions, and this can mess up your penetration front.You can use Liquid phase compressibility property to help this for steep front startup.
Are you getting stagnant calculations with time-step decreases but not change in iteration history? Problem is that you have lost your capacitance term. Compressibility of the liquid is sometimes a remedy, but also a more accurate predictor. Mass lumping can help too and accomplishes the same thing. Sometimes your initial time step can be too small for a good start. Try increasing it …
-Another startup issue: Steep discontinuities at boundaries and internally for initial conditions are bad, obviously. If your time step is such that the front cannot penetrate beyond one element in one time step, then with linear elements the capacitance term is ineffective (small) upon reduced time steps. Somehow you have got to get the front beyond one or two elements before things work properly. I find that ramping up the initial boundary conditions helps. Sometimes a large first time step to kick it is good too.
-On startup of a pressurized column of liquid penetrating into a porous substrate, I noticed that at zero-based p_liq, there was no problem elevating the applied pressure on the penetration, but at Atm-based p_liq we couldn’t start the problem without severe compressibility. However, compressibility affects the solution, and in fact allows you to push all of your column of liquid into a compressed layer in the substrate, with no Sat from propagation. So beware of poorly defined compressibility of liquid. Also, refinement in the porous layer helped the startup. But the most significant thing for the problem I was solving, don’t be surprised if just a little perturbation on externally applied pressure greatly affects the penetration rate. In fact, in one problem simply changing from p_ext of 1.01325e+6 to 1.11325+6 increases the penetration rate 2-fold initially. The steeper curves are harder to handle.
References#
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk
