Saturation#

Saturation = {model_name} {float_list} []

Description / Usage#

This card specifies the model for the liquid saturation in a partially saturated porous media, which is frequently observed experimentally to be a function of the capillary pressure (gas pressure minus liquid pressure). This card is required for Media Type specifications of POROUS_PART_SAT, POROUS_UNSAT, and POROUS_TWO_PHASE. Definitions of the input parameters are as follows:

{model_name}

Name of the model for the liquid in a partially saturated porous media. The permissible values are CONSTANT,VAN_GENUCHTEN, TANH, PSD_VOL, PSD_WEXP, and PSD_SEXP.

{float_list}

One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}.

Saturation model choices and their parameters are discussed below.

CONSTANT <float1>

For the constant value of saturation model. This model is rarely used, unless one wanted to study the flow of gas and liquid at some constant, pre-specified saturation as a function of gas and liquid phase pressure.

VAN_GENUCHTEN

The VAN_GENUCHTEN model assumes that saturation is a function of the capillary pressure. The {float_list} contains four values, where:

  • <float1> - Irreducible water saturation

  • <float2> - Irreducible air saturation

  • <float3> - An exponent β

  • <float4> - A scaling to convert from capillary pressure to suction (α ⁄ ρl ⁄g)

TANH <float_list>

The first version of the TANH model assumes that saturation is only a function of capillary pressure. The {float_list} contains four values, where:

  • <float1> - Irreducible water saturation, θw

  • <float2> - Irreducible air saturation, θair

  • <float3> - A constant c

  • <float3> - A constant d

PSD_VOL <float1> <float2>

This model can only be used in conjunction with the same model for permeability and relative liquid permeability; two input values are required:

  • <float1> - Surface tension of the liquid

  • <float2> - Contact angle the liquid-vapor menisci makes with the solid surfaces

PSD_WEXP <float1> <float2>

This model can only be used in conjunction with the same model for permeability and relative liquid permeability; two input values are required:

  • <float1> - Surface tension of the liquid

  • <float2> - Contact angle the liquid-vapor menisci makes with the solid surfaces

PSD_SEXP <float1> <float2>

This model can only be used in conjunction with the same model for permeability and relative liquid permeability; two input values are required:

  • <float1> - Surface tension of the liquid

  • <float2> - Contact angle the liquid-vapor menisci makes with the solid surfaces

Examples#

Following is a sample card:

Saturation = VAN_GENUCHTEN 0.01 0.01 3.9 1.

The parameters on this VAN_GENUCHTEN specification are basically curve fit parameters to experimental measured saturation values versus capillary pressure. They do have some physical meaning, as is described below, and in the references.

Technical Discussion#

The saturation function specification is perhaps the most critical and most influential function for capturing accurate behavior of flow through partially saturated porous media. The basic cap of this function versus capillary pressure is depicted in the figure below: Notice the plateau of saturation at unity at low capillary pressures (high positive liquid pressures) and the dip to the irreducible water saturation at high capillary pressures. In most real operations, this dependence will be highly sensitive to many factors: viz. whether you are filling or vacating the pore space, whether network stress in poroelastic problems is leading to liquid tension, etc.

The Van Genuchten model has the following functional form:

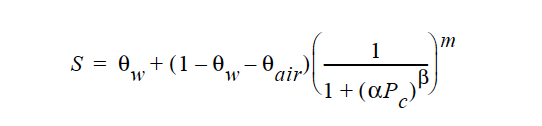
../../_images/415_goma_physics.png

Here the irreducible water saturation is θw, the irreducible air saturation 0air, the suction factor is α, and the exponents β and m, the latter of which is 1 – 1 ⁄ β.

The TANH model has the following functional form:

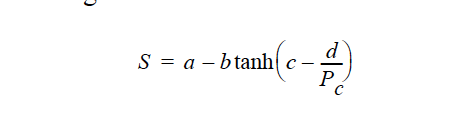
../../_images/416_goma_physics.png

where a and b are automatically calculated from

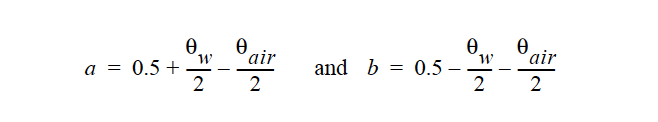
../../_images/417_goma_physics.png

and c and d are two fitted coefficients provided as input parameters. Here the irreducible water saturation is 0w, the irreducible air saturation 0air, and are also provided by the user as input parameters. Pc is the capillary pressure which has a lower limit of 1.E-5.

References#

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk.

GTM-029.0: SUPG Formulation for the Porous Flow Equations in Goma, H. K. Moffat, August 2001 (DRAFT).

SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996).