Default Material Species Type#
Default Material Species Type = {species_type_string}
Description / Usage#
This optional parameter sets the form of the species variable type within Goma. Valid options for {species_type_string} are given below by the SPECIES_* names (along with a description and variable (prefix) name:
SPECIES_MASS_FRACTION |
Mass Fractions |
Yk_ |
SPECIES_MOLE_FRACTION |
Mole Fractions |
Xk_ |
SPECIES_VOL_FRACTION |
Volume Fractions |
Vk_ |
SPECIES_DENSITY |
Species Densities |
Dk_ |
SPECIES_CONCENTRATION |
Species Concentration |
Ck_ |
SPECIES_UNDEFINED_FORM |
Undefined form |
Y |
The default is to assume SPECIES_UNDEFINED_FORM. Please refer to the Technical Discussion for important details.
Examples#
Following is a sample card:
Default Material Species type = SPECIES_MASS_FRACTION
Technical Discussion#
For nondilute systems the SPECIES_ quantities above are not just simply interchangeable via a multiplicative constant. Their values are distinct, and their interrelationship evaluated via a potentially nontrivial equation of state. Prior to the implementation of this card/capability, Goma hadn’t handled many nondilute cases, and where it had, this issue was finessed by special casing property evaluations.
This card both sets the type of the species variables and establishes a convention for the units of equations within Goma. For settings of SPECIES_MASS_FRACTION and SPECIES_DENSITY_FRACTION, equations generally have a mass unit attached to them. Equations have concentration units attached to them for settings of SPECIES_MOLE_FRACTION, SPECIES_VOL_FRACTION, and SPECIES_CONCENTRATION. For example, given a setting of SPECIES_MASS_FRACTION, each volumetric term in the species conservation equation has units of mass per time, i.e., the time derivative term is written as
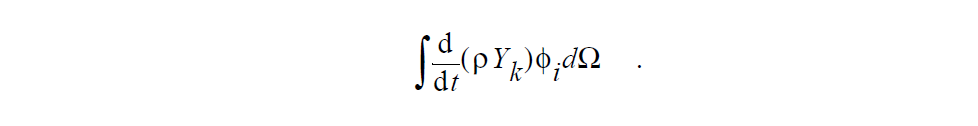
For a setting of SPECIES_MOLE_FRACTION, each volumetric term would have units of moles per time, i.e., the time derivative term is written out as
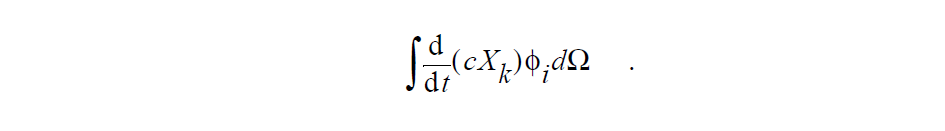
All this is necessary in order to handle cases where the total density or total concentration of a phase is spatially variable. In that case, it can’t just be divided out as in earlier versions of Goma but must be included in the conservation equations, and therefore the units of the conservation equation must reflect this.
The species variable type affects the units and thus values of quantities returned from certain boundary conditions. For example, the IS_EQUIL_PSEUDORXN boundary condition returns units of moles per time per \(length^2\) if the species variable type is defined to be SPECIES_CONCENTRATION, but will multiply by molecular weights and thus return units of mass per time per \(length^2\) if the species variable type is defined to be SPECIES_MASS_FRACTION. This change conforms to the expected units of the overall species conservation equation for the two values of the species variable type variable used as examples above.
The last column in the table above contains a three letter string. This string is used as a prefix for the name of the species variable in the EXODUS output file. If no names are specified in the material file and Chemkin is not used (which provides names for the species variables itself), then integers are used for names. For example, the first species unknown in Goma problem employing Mass Fractions as the independent species variables will be called Yk_1. If Chemkin is used in the same problem and the first chemkin species is named H2O, then the name in the EXODUS output file will be Yk_H2O. If a Goma problem is solved with no specification of the type of the species variable, then the first unknown in the EXODUS file will be named Y1.
Additionally, some boundary conditions and inputs from the material file section will set the species variable type on their own without the benefit of this card, if the species variable type is the default undefined form. Some internal checks are done; if an inconsistency is caught, Goma will abort with an informative error message.