Rel Liq Permeability#

Rel Liq Permeability = {model_name} {float_list} []

Description / Usage#

This card is required for Media Type POROUS_TWO_PHASE. This card specifies the model for the relative liquid phase permeability for flow in a partially saturated porous media, such that the liquid flow is the pressure gradient in the liquid times the permeability times the relative liquid phase permeability divided by the liquid viscosity. Definitions of the input parameters are as follows:

{model_name}

Name of the model for the relative gas phase permeability; the permissible values are CONSTANT, VAN_GENUCHTEN, PSD_VOL, PSD_WEXP, and PSD_SEX.

{float_list}

One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}.

Permeability model choices and their parameters are discussed below.

CONSTANT <float1>

a constant relative liquid permeability; this is a rarelyused option.

  • <float1> - relative liquid permeability, obtained by dividing the relative permeability desired by the liquid-phase viscosity

VAN_GENUCHTEN <float1> <float2> <float3> <float4>

assumes that the relative liquid permeability is a function of the saturation (as specified in the Saturation card). The {float_list} contains four values for this model, where:

  • <float1> - Irreducible water saturation

  • <float2> - Irreducible air saturation

  • <float3> - Exponent ( λ = 1 – 1 ⁄ β ) in krel model

  • <float4> - Liquid viscosity

PSD_VOL <float1>

This model can only be used in conjunction with the same model for permeability and saturation; a single input value isrequired:

  • <float1> - Liquid phase viscosity

All other parameters are loaded up from the Saturation and Permeability cards.

PSD_WEXP <float1>

This model can only be used in conjunction with the same model for permeability and saturation; a single input value is required:

  • <float1> - Liquid phase viscosity

PSD_SEXP <float1>

This model can only be used in conjunction with the same model for permeability and saturation; a single input value is required:

  • <float1> -Liquid phase viscosity

Examples#

Following is a sample card:

Rel Liq Permeability = VAN_GENUCHTEN 0.01 0.01 0.667 0.01

Technical Discussion#

The most often used model is that of VAN_GENUCHTEN. The functional form of this model is as follows:

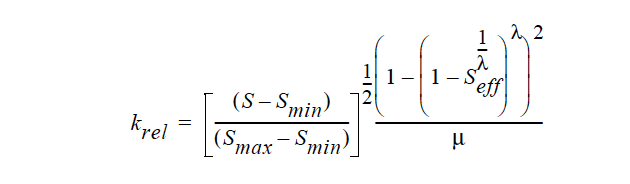
../../_images/413_goma_physics.png

where

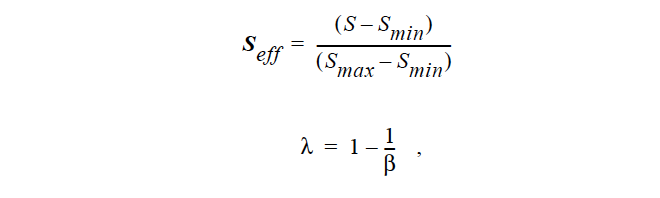
../../_images/414_goma_physics.png

and is the viscosity. This function is clipped to zero as and clipped to one as Seff → 1. PSD_* model theory details can be found in the references cited below. These models bring in more explicit dependence on pore size and size distribution, as well as other microstructural features. In the VAN_GENUCHTEN model, such parameter effects are embodied in the Saturation dependence, which is empirically fit through the saturation function.

References#

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk

SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)