Convective Lagrangian Velocity#
Convective Lagrangian Velocity = {model_name} {float_list} [L/t]
Description / Usage#
In solid mechanics, when the deformation of the mesh is Lagrangian, i.e., motion of the solid can be described by a mapping from the stress-free state (undeformed state) to the deformed state, it is often desirable to prescribe a convective velocity of the stress-free state that can lead to inertial forces through deformation (see Technical Discussion below). This required card allows for the specification of solid-body translation or rotation of the stress-free state, and results in an inertial term on the otherwise quasi static solid momentum equation.
Definitions of the input parameters are as follows:
{model_name} |
Name of the prescribed velocity model. This parameter can have one of the following values: NONE, CONSTANT, or ROTATIONAL. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model below. Note that not all models employ a {float_list}. |
Thus,
NONE |
the stress-free state is assumed to be unmoving. No floating point input values are required with this model. |
CONSTANT <float1> <float2> <float3> |
the stress-free state is one of solid-body translation, viz. it moves uniformly with a velocity specified by three orthogonal components:
|
ROTATIONAL <float1> <float2> <float3> <float4> |
the stress-free state is one of solid-body rotation at a specified rotation rate.
Note that this model is applicable in 2-D and certain 3-D problems in which the rotation axis is the Z-axis. To generalize this model to three-dimensions, the proper input will require a point and a direction of the rotation axis. In two-dimensions, the axis of rotation is the Z-direction. |
Examples#
The following is a sample input card:
Convective Lagrangian Velocity = ROTATIONAL 25.0 1. 1. 0.
This card is associated with a material file, and hence a material that is of LAGRANGIAN or TOTAL_ALE type (see Mesh Motion card). That material’s stressfree state, as specified by this model, will rotate about an axis that is located at [1.0, 1.0, 0] at 25 radians/sec (assuming seconds are the time scale of the problem).
Technical Discussion#
This capability is often used when problems require a force or a boundary condition to be applied to a solid material that is moving relative to the source, or the desired frame of reference. Such constraints arise mainly in fluid-structure interaction problems where one solid material is moving relative to another, with a fluid material in between, e.g. deformable blade or knife metering/pushing liquid over a flat or round substrate. These models have also been used in porous-material translation relative to a drying source (see references below).
Specification of any model but NONE on this card produces the left-hand-side term in the equation for quasi static equilibrium:
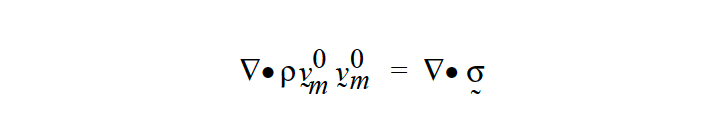
\(\sigma\) is the Cauchy stress tensor of the solid material, and f is the body force per unit volume. The first term is a result of the specified advection of the stress-free state. \(v_m^0\), which depends solely on the user-prescribed velocity and the current state of deformation, is by definition
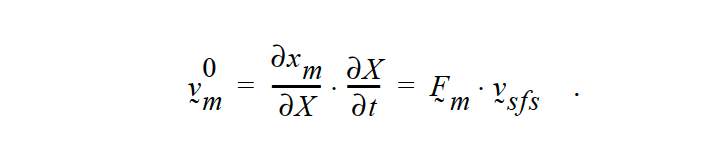
where \(F_m\) is the material deformation gradient tensor (computed somewhat differently depending on the formulation, as described in the references below), and \(v_sfs\) is the stress-free state velocity field specified by this card.
References#
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk
SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk (May 2000)
