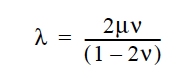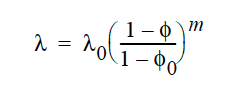Lame LAMBDA#

Lame LAMBDA = {model_name} {float_list} [M/Lt2]

Description / Usage#

This required card is used to specify the model for the Lame coefficient λ for the solid constitutive equation (see Sackinger, et. al., 1995). When using a nonlinear constitutive equation for ALE mesh motion, this coefficient is related to the bulk modulus:

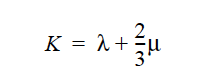
../../_images/366_goma_physics.png

Definitions of the input parameters are as follows:

{model_name}

Name of the Lame LAMBDA model. This parameter can have one of the following values: CONSTANT, POWER_LAW, EXPONENTIAL or USER.

{float_list}

One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model below.

The models are described here.

CONSTANT <float1>

For the CONSTANT model, {float_list} is a single value (see Lame MU card for relationship to other more common elastic constants):

  • <float1> - Standard value of the elastic constant \(\lambda\)

POISSON_RATIO <float1>

For any Lame MU model (see Lame MU card) this option uses the following formula to compute Lame Lame LAMBDA:

  • <float1> - Poisson’s ratio nu.

../../_images/367_goma_physics.png

POWER_LAW <float1> <float2> <float3>

The POWER_LAW model can be used in deformable porous media where the Lame coefficient varies as a power of the porosity, \(\phi\) (Scherer, 1992):

../../_images/368_goma_physics.png

The {float_list} contains three values for this model, where:

  • <float1> - \(\lambda_0\) is the base Lame LAMBDA modulus at the initial porosity.

  • <float2> - \(\phi_0\) is the porosity in the stress-free state

  • <float3> - m is the powerlaw exponent, as shown

USER <float1>,…, <floatn>

For the USER model, {float_list} is of arbitrary length, and the values are used through the param[] array in usr_lame_lambda function to parameterize a userdefined model. See examples in user_mp.c.

Examples#

Following is a sample card:

Lame LAMBDA = CONSTANT 1.

Technical Discussion#

Please see the Solid Constitutive Equation card for details on the use of this parameter. Special consideration is required for INCOMP* type constitutive equations. The isotropic stress term, or pressure, in that case is added onto the constitutive equation, and so this parameter must be set to zero so as to prevent any compressibility.

Important note that when one desires an incompressible solid through the use of INCOMP_PSTRAIN type models, by using an incompressible continuity equation in a LAGRANGIAN mesh region (see EQ = continuity), then the bulk modulus, or Lame Lambda expansion term is also added on. So to get a truly incompressible response, one must set the Lame LAMBDA coefficient to zero.

References#

Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.

Scherer, G.W., 1992, “Recent Progress in Drying of Gels”, J. of Non-Crystalline Solids, 147&148, 363-374

GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche

SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)