shell_energy#

EQ = shell_energy {Galerkin_wt} SH_T {Interpol_fnc} <floatlist>

Description / Usage#

This card provides information for solving a shell thermal energy equation. Use of this equation can be made for any shell, including those which involve Reynold’s film or confined flow lubrication flow. Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be set the same for the code to work properly.

shell_energy

Name of equation to be solved.

{Galerkin_wt}

Two-or four-character value that defines the type of weighting function for this equation, where:

  • Q1–Linear

  • Q2–Quadratic (not recommended at this time)

SH_T

Name of the variable associated with this equation.

{Interpol_fnc}

Two-or four-character value that defines the interpolation function for the variable SH_T, where:

  • Q1–Linear

  • Q2–Quadratic (not recommended at this time)

<float1>

Multiplier for the mass matrix term.

<float2>

Multiplier for the advection term.

<float3>

Multiplier for the boundary term (not used).

<float4>

Multiplier for the source term.

Examples#

Following is a sample card:

EQ = shell_energy Q1 SH_T Q1 1. 1. 1. 1. 1.

This applies the shell energy equation with all terms activated on a SHELL4 or BAR2 mesh.

Technical Discussion#

The equation solved is as follows:

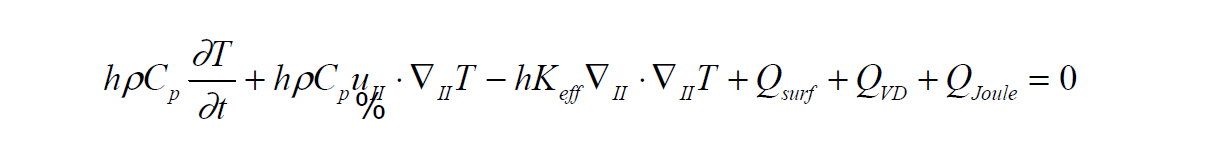
../../_images/312_goma_physics.png

  • Clearly this equation looks similar to the standard energy equation for continuum formulations, but the presence of the gap/film thickness h indications that the assumption of a constant shell temperature across the thickness is assumed, and hence all the terms are constant in that integrated direction. The source terms are all invoked in the material files, and there are many types and many submodels.

  • Special NOTE: This equation can be up-winded for high Peclet number flows. If the Energy Weight Function card in the companion material file is set to SUPG, then the advection term is stabilized with standard streamwise-upwinding-Petrov- Galerkin approach.