Adaptive Viscosity Scaling#

Adaptive Viscosity Scaling = CONSTANT <float>

Description / Usage#

This optional card is used to specify the adaptive viscosity scaling and the ε parameter associated with its usage (see theory section below). It requires one floating point number that scales the term. Definitions of the input parameters are as follows:

CONSTANT

Name of the model for the adaptive viscosity scaling.

  • <float> - value of ε scaling parameter.

Examples#

The following is a sample card that sets the adaptive viscosity scaling to 0.5:

Adaptive Viscosity Scaling = CONSTANT 0.5

Technical Discussion#

The momentum equation is modified with the addition of a numerical adaptive viscosity to help maintain the elliptic character of the equation set as stress and velocity gradient increase

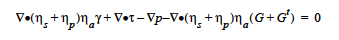
../../_images/393_goma_physics.png

where ηs is the solvent viscosity and ηp is the polymer viscosity. If we set the adaptive viscosity to zero (ηa= 0), we obtain the Standard EVSS Formulation of Guenette and Fortin (1995). For adaptive viscosity, we use the following definition

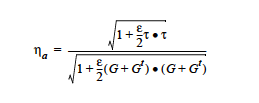
../../_images/394_goma_physics.png

with 0<ε<1.

The equations are unchanged in the limit of h, the element size, going to zero.

Please see the viscoelastic tutorial for a discussion of usage for the adaptive viscosity scaling. The papers by Sun, et. al. (1996) and Sun, et. al (1999) provide a good discussion of the theory behind its usage. CRMPC presentations by R.R. Rao demonstrates its usefulness for Goma calculations.

References#

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

Guenette, R. and M. Fortin, “A New Mixed Finite Element Method for Computing Viscoelastic Flows,” J. Non-Newtonian Fluid Mech., 60, 27-52 (1995).

Sun, J., N. Phan-Thien, R. I. Tanner, “An Adaptive Viscoelastic Stress Splitting Scheme and Its Applications: AVSS/SI and AVSS/SUPG,” J. Non-Newtonian Fluid Mech., 65, 75-91 (1996).

Sun, J., M. D. Smith, R. C. Armstrong, R. A. Brown, “Finite Element Method for Viscoelastic Flows Bases on the Discrete Adaptive Viscoelastic Stress Splitting and the Discontinuous Galerkin Method: DAVSS-G/DG,” J. Non-Newtonian Fluid Mech., 86, 281-307 (1999).