shell_surf_div_v#

EQ = shell_surf_div_v {Galerkin_wt} gamma1 {Interpol_fnc} <float1>

Description / Usage#

This card provides information for solving a definition equation for surface divergence of the fluid velocity field on a 2-dimensional bar element. Note that this equation is not yet available in three dimensions. This term is required by the non-Newtonian surface rheology capability in Goma. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly. Also note that this term is not currently active in Goma, and the developers should be consulted.

shell_surf_div_v

Name of the equation to be solved.

{Galerkin_wt}

Two- or four-character value that defines the type of weighting function for this equation, where:

  • Q1-Linear

  • Q2-Quadratic

gamma1

Name of the variable associated with the shell curvature equation.

{Interpol_fnc}

Two- or four-character value that defines the interpolation function used to represent the variable K where:

  • Q1-Linear Continuous

  • Q2-Quadratic Continuous

<float1>

Multiplier on whole equation. Set to 1.0.

Examples#

The following is a sample card that uses linear continuous curvature interpolation and weight function:

EQ = shell_surf_div_v Q1 gamma1 Q1 1.0

Technical Discussion#

This shell equation is required for proper computation of the Boussinesq-Scriven surface rheological constitutive equation (namely the surface divergence of the velocity field in the 4th and 6th terms on the right of the following equation). The functional form of this equation is as follows:

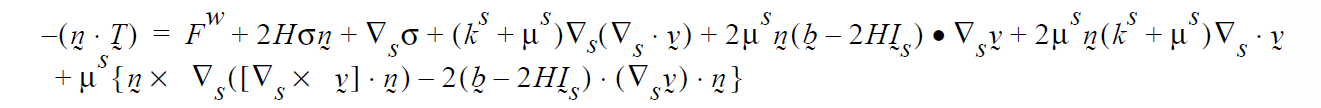
../../_images/305_goma_physics.png

Here, \(\Delta_s\) \(\equiv\) (\(\underline{I}\) – \(\underline{n}\) \(\underline{n}\)) ⋅ \(\Delta\) is the surface gradient operator, and \(I_s\) \(\equiv\) (\(\underline{I}\) – \(\underline{n}\) \(\underline{n}\)) is the surface unit tensor. \(\mu_s\) and \(\kappa_s\) are the surface shear viscosity and surface extensional viscosity, respectively. Note that the first three terms on the right are balance of the stress in the standard Goma CAPILLARY condition, with surface tension gradients being accommodated through variable surface tension. The boundary condition CAPILLARY_SHEAR_VISC is used to set the additional terms of this constitutive equation. As of January 2006 only the 7th term on the right hand side is implemented, as it is the only nonzero term in a flat surface shear viscometer. The building blocks for the other terms are available through additional shell equations. These remaining terms actually represent additional dissipation caused by surface active species microstructures flowing in the surface. The best source of discussion of this equation is a book by Edwards et al. (1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston).

References#

Edwards, D. A., Brenner, H., Wasan, D. T., 1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston.