Category 10: Gradient Equations#
As companion equations to the viscoelastic stress equations, a continuous velocity gradient is determined through the so-called Velocity Gradient Equations. These boundary conditions are of the Dirichlet type and can be used to put conditions on this class of equations.
G11#
BC = G11 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT11)
This Dirichlet boundary condition specification is used to set a constant xx-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G11 |
Boundary condition name (<bc_name>) that defines the xx-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of xx-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the xx-velocity gradient component on node set 100:
BC = G11 NS 100 5.0
BC = G11 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:
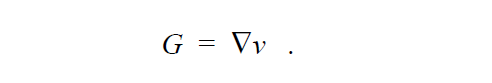
Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G12#
BC = G12 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT12)
This Dirichlet boundary condition specification is used to set a constant xy-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G12 |
Boundary condition name (<bc_name>) that defines the xy-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of xy-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
Following is a sample card for applying a Dirichlet condition on the xy-velocity gradient component on node set 100:
BC = G12 NS 100 5.0
BC = G12 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:
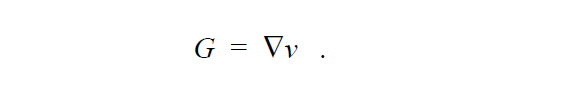
Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G13#
BC = G13 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT13)
This Dirichlet boundary condition specification is used to set a constant xz-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G13 |
Boundary condition name (<bc_name>) that defines the xz-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of xz-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the xz-velocity gradient component on node set 100:
BC = G13 NS 100 5.0
BC = G13 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:
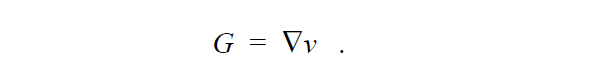
Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G21#
BC = G21 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT21)
This Dirichlet boundary condition specification is used to set a constant yx-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G21 |
Boundary condition name (<bc_name>) that defines the yx-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of yx-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the yx-velocity gradient component on node set 100:
BC = G21 NS 100 5.0
BC = G21 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G22#
BC = G22 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT22)
This Dirichlet boundary condition specification is used to set a constant yy-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G22 |
Boundary condition name (<bc_name>) that defines the yy-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of yy-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the yy-velocity gradient component on node set 100:
BC = G22 NS 100 5.0
BC = G22 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:
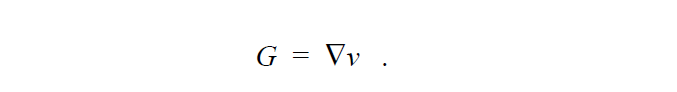
Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G23#
BC = G23 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT23)
This Dirichlet boundary condition specification is used to set a constant yz-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G23 |
Boundary condition name (<bc_name>) that defines the yz-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of yz-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the yz-velocity gradient component on node set 100:
BC = G23 NS 100 5.0
BC = G23 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:
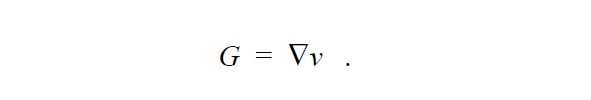
Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G31#
BC = G31 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT31)
This Dirichlet boundary condition specification is used to set a constant zx-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G31 |
Boundary condition name (<bc_name>) that defines the zx-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of zx-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the zx-velocity gradient component on node set 100:
BC = G31 NS 100 5.0
BC = G31 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:
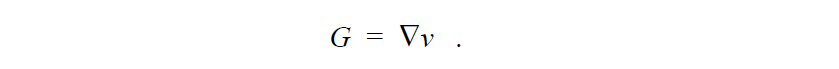
Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G32#
BC = G32 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT32)
This Dirichlet boundary condition specification is used to set a constant zy-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G32 |
Boundary condition name (<bc_name>) that defines the zy-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of zy-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the zy-velocity gradient component on node set 100:
BC = G32 NS 100 5.0
BC = G32 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:
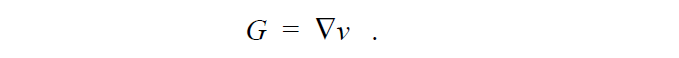
Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
G33#
BC = G33 NS <bc_id> <float1> [float2]
Description / Usage#
(DC/GRADIENT33)
This Dirichlet boundary condition specification is used to set a constant zz-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:
G33 |
Boundary condition name (<bc_name>) that defines the zz-velocity gradient. |
NS |
Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. |
<bc_id> |
The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. |
<float1> |
Value of zz-velocity gradient. |
[float2] |
An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences. |
Examples#
The following is a sample card for applying a Dirichlet condition on the zz-velocity gradient component on node set 100:
BC = G33 NS 100 5.0
BC = G33 NS 100 5.0 1.0
where the second example uses the “residual” method for applying the same Dirichlet condition.
Technical Discussion#
We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.
See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).
References#
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
