Heat Source#
Heat Source = {model_name} <float_list> [varies]
Description / Usage#
This required card is used to specify the model for the source term on the energy equation. Definitions of the input parameters are as follows:
{model_name} |
Name of the model for the source term on the energy equation. The permissible values are
|
<float_list> |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. Note that not all models have a <float_list>. |
Source-term model choices and their parameters are discussed below. WARNING: make sure the equation term multipliers for the source terms are set to unity (see the Equation Cards segment in the previous chapter).
CONSTANT <float1> |
The constant source model adds a constant homogenous source term [E/L3t] to the heat equations. The <float_list> has a single value: <float1> - Heat source. |
USER <float1>… <floatn> |
The USER option indicates that a user-defined model has been introduced into the usr_heat_source routine in the user_mp.c file. The <float_list> is of arbitrary length subject to the user’s requirements to parameterize the model. |
USER_GEN <float1>… <floatn> |
The USER_GEN option provides a user-defined model with low-level, general capabilities. For this option one must make the appropriate modifications to the routine usr_heat_source_gen in the user_mp_gen.c file. The difference between the USER and USER_GEN capabilities is described at the beginning of this chapter. |
JOULE |
The JOULE model is used to specify a Joule heating source term. No input is required for this model as the sole independent parameter of the model for the voltage equation is the “Electrical Conductivity”, which is specified in the material file. |
EPOXY <float1> |
The EPOXY model is used to specify the heat generated by an epoxy curing reaction. The single input value is the:
|
VISC_DISS <float> |
The VISC_DISS model is used to specify the heat generated by viscous dissipation. The <float_list> has a single value:
|
BUTLER_VOLMER <integer> <float1> <float2> <float3> <float4> <float5> <float6> <float7> <float8> |
The BUTLER_VOLMER model is used to specify the current source or sink due to a homogeneuous electrochemical reaction involving a single species (e.g., the hydrogen oxidation and oxygen reduction reactions in a hydrogen-feuled polymerelectrolyte- membrane fuel cell), which is computed using the Butler-Volmer kinetic model (as described in the Theory section of the BUTLER_VOLMER current source card). This is due to that the voltage equation is used to solve for the electrical potential in the liquid electrolyte phase whereas the energy equation is utilized to solve for the electrical potential in the solid-electrode phase such that the electrode potential unknowns is represented by the temperature unknown. Parameters required for this BUTLER_VOLMER heat source model are the same as those for the BUTLER_VOLMER current source model; accordingly, detailed description of the model parameters can be found in the Current Source section of this manual. |
ELECTRODE_KINETICS |
The ELECTRODE_KINETICS model is used to specify the current generated or consumed in the solid electrode phase in electrochemical processes involving concentrated electrolyte solution and multiple species as in thermal batteries. As in the case of the BUTLER_VOLMER model, this is due to that the voltage equation is used to solve for the electrical potential in the liquid electrolyte phase whereas the energy equation is utilized to solve for the electrical potential in the solid- electrode phase such that the electrode potential unknowns is represented by the temperature unknown. The {model_name} ELECTRODE_KINETICS toggles on the option in the equation assembly; no parameters are required. |
Examples#
The following is a sample input card:
Heat Source = CONSTANT 1.
Technical Discussion#
The energy equation solved by Goma, which can be found elsewhere, is a convectionconduction equation given by
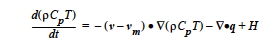
The heat source-term model represented by H is specified by this input record. The CONSTANT, USER and USER_GEN options provide the standard means of specifying model input and will not be discussed.
JOULE Model: The JOULE model is used to specify a Joule heating term. It is based on heat generation in a medium of specified electrical resistance subjected to an electrical voltage potential. It computes the heat source as:
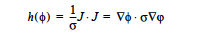
where J is the current flux density which is represented as –σ∇φ and φ is represented using the voltage equation. No input is required for this model since the Electrical Conductivity is specified in the material file for the voltage equation.
EPOXY Model: The EPOXY model is used to specify the heat generated by a condensation reaction, which is the heat of reaction, ΔHrxn, multiplied by the reaction rate as measured by the extent of reaction. The form of the equation is:
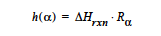
This card is used in conjunction with the EPOXY Species Source so that the reaction rate Rα can be determined.
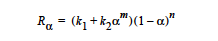
VISC_DISS Model: In heat transfer problems that are accompanied by fluid flow, the energy balance equation contains a term which represents the (rate of) work done on the fluid by viscous forces. These forces have the potential to raise the fluid temperature and therefore it may be necessary to include these forces in your analysis. Typically, problems in which this term is significant may be characterized as highspeed flows with large velocity gradients, rapid extrusion and lubrication problems. The Brinkman number (Br = (μV2) ⁄ (kΔT)) is an indicator of the importance of viscous heating relative to the heat flow caused by temperature gradients.
Mathematically, the Heat Source term, H, in the energy equation is given by
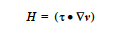
where (( •) indicates a double dot product. This mechanism is an irreversible process whereby mechanical energy is degraded into thermal energy, as the right hand side expands to the sum of quadratic terms which will always be positive, at least for Newtonian fluids. In Goma, the VISC_DISS model computes the source term in function visc_diss_heat_source in mm_std_models.c; the expression looks like
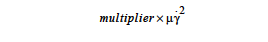
where μ is the viscosity and γ is the shear rate.
The multiplier allows the user the flexibility to choose appropriate units for the momentum and energy equations. For example, for many problems the momentum equations are scaled appropriately using viscosity units of psi-sec. But in the absence of this multiplier, this would force the energy equation to be in units of psi/sec; in other words, (density*heat capacity) would need to be in units of psi/(deg C) and thermal conductivity would need to be in units of psi-in2/(sec-deg C) - these aren’t exactly common units! Instead, we can set the multiplier to 6891 (i.e., 6891 Pa = 1 psi) in order to have the energy equation in units of J/sec - i.e. leaving (density*heat capacity) in units of J/(m3 deg C) and thermal conductivity in terms of J/(m-sec deg C). Another use of the multiplier is to allow appropriate scales when the momentum equation is diffusion-dominated and the thermal equation is convection-dominated. Suppose we keep all quantities in MKS units. The convection terms in the thermal equation can then be scaled to roughly order unity by dividing through by (density*heat capacity) - i.e. set heat capacity=1/density, thermal conductivity = thermal diffusivity, and set the dissipation multiplier to 1/(density*heat capacity).
So, in essence, this multiplier allows flexibility in the choice of mechanical and thermal units in a convenient manner - i.e. it’s on the term that couples the energy and momentum equations.
BUTLER_VOLMER and ELECTRODE_KINETIC Models: As mentioned above, these two models are used to specify the current generated or consumed in the solid electrode phase in electrochemical processes such as polymer-electrolyte-membrane fuel cells and thermal batteries. This is due to that the voltage equation is used to solve for the electrical potential in the liquid electrolyte phase whereas the energy equation is utilized to solve for the electrical potential in the solid-electrode phase such that the electrode potential unknown is actually represented by the temperature unknown. Further details for the BUTLER_VOLMER model are presented in the current source model section of this manual and that for the ELECTRODE_KINETIC model can be found in the reference provided below (Chen et al. 2000).
VARIABLE_DENSITY Model: Work was begun on a VARIABLE_DENSITY model for drying problems but has not been completed. The roots for this may be found in the source code but the model is not yet functional; it was not listed above as a valid Heat Source option.
References#
SAND2000-0207: Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions, K. S. Chen, G. H. Evans, R. S. Larson, D. R. Noble and W. G. Houf, January 2000.
