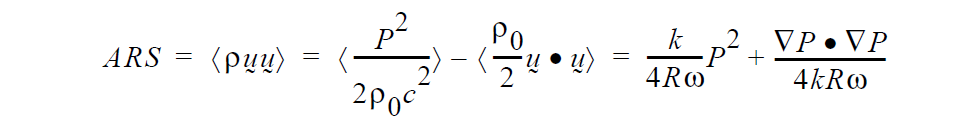acous_reyn_stress#
EQ = acous_reyn_stress {Galerkin_wt} ARS {Interpol_fnc} <float list>
Description / Usage#
This card provides information for solving a differential equation for the Reynolds stress that results from time averaging of the acoustic pressure and velocity fields. Interactions of the fluid momentum equations with the acoustic wave equations are then afforded through gradients of the scalar acoustic Reynolds stress with the use of the ACOUSTIC Navier-Stokes source. Definitions of the input parameters are defined below. Note that <float1> through <float3> define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
acous_reyn_stress |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
ARS |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable SH, where:
|
<float1> |
Multiplier for the Reynolds stress variable. |
<float2> |
Multiplier for the kinetic energy term. |
<float3> |
Multiplier for the compressional energy term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples#
The following is a sample card that uses quadratic continuous interpolation for the acoustic Reynolds stress equation and turns on all the term multipliers:
EQ = acous_reyn_stress Q2 ARS Q2 . 1. 1. 1.
Technical Discussion#
The Reynolds stress due to acoustic fields reduces to a combination of compressional and kinetic energy terms which can be expressed in terms of the magnitude of the acoustic pressure and its gradient. P is the amplitude of the acoustic pressure (complex), k is the wavenumber, R is the acoustic impedance, and \(\omega\) is the frequency (rad/sec).