Electrical Conductivity#
Electrical Conductivity = {model_name} {float} []
Description / Usage#
This required card is used to specify the model for electrical conductivity. There are currently three options, so {model_name} can be either CONSTANT, ELECTRONEUTRALITY_FICKIAN or ELECTRONEUTRALITY_SM. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for constant electrical conductivity. <float> - the value of electrical conductivity. |
LEVEL_SET |
Name of the model for constant electrical conductivity.Allows for the conductivity as a function of the level-set field. Specifically used for changing the conductivity from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
ELECTRONEUTRALITY_FICKIAN |
Name of the model for the electrical conductivity. This model requires no parameter specification, i.e. no floats. |
ELECTRONEUTRALITY_SM |
Name of the model for the electrical conductivity. This model requires no parameter specification, i.e. no floats. In earlier versions of Goma, this model was referred to by the name ELECTRODE_KINETICS and it remains to be active so that Goma can be backward compatible. In other words, ELECTRONEUTRALITY_SM and ELECTRODE_KINETICS are interchangeable. |
See Technical Discussion for information on the electrical conductivity for the two models of ELECTRONEUTRALITY.
Examples#
Following are sample cards:
Electrical Conductivity = CONSTANT 1.
Electrical Conductivity = ELECTRONEUTRALITY_FICKIAN
Electrical Conductivity = ELECTRONEUTRALITY_SM
Electrical Conductivity = ELECTRODE_KINETICS
Technical Discussion#
For concentrated electrolyte solutions in which Stefan-Maxwell flux equations are employed to relate species fluxes to concentrations and their gradients, the electrical conductivity is given by (Chen et al. 2000, Schunk et al. 2000):
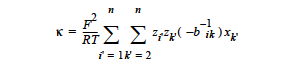
where i = m(i’ – 1) + 1 and k = m(k’ – 1) + 1, m is dimension of the problem (m = 2 for a 2-D problem), and is species mole fraction. The tedious definition of can be found in Chapter 2 of Chen et al. (Chen et al. 2000) and in Chapter 7 of the Goma Developer’s Guide (Schunk, et. al., 2000).
For dilute electrolyte solutions in which Fick’s first law is used to relate the flux of a species to its concentration gradient, the electrical conductivity is given by (Chen, 2000; Schunk, et. al., 2000):
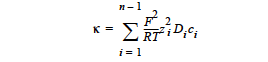
where ci is the molar concentration and zi is the charge number of species i, respectively; and n is the total number of species present in the electrolyte solution. Note that the nth species is taken to be the neutral solvent species, which has no contribution to the electrical conductivity since its charge number is zero.
Lastly, Goma calculates the conductivity in function assemble_potential as material properties are being loaded.
References#
GTM-025.0: Chen, K. S., “Modeling diffusion and migration transport of charged species in dilute electrolyte solutions: GOMA implementation and sample computed predictions from a case study of electroplating”, Sandia technical memorandum, September 21, 2000.
SAND2000-0207: Chen, K. S., Evans, G. H., Larson, R. S., Noble, D. R., and Houf, W. G., “Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions”, Sandia Technical Report, 2000.
GDM-1.3: Schunk, P. R., Sackinger, P. A., Rao, R. R., Subia, S. R., Baer, T. A., Labreche, D. A., Moffat, H. K., Chen, K. S., Hopkins, M. M., and Roach, R. A., “GOMA 3.0 - A Full-Newton Finite Element Program for Free and Moving Boundary Problems with Coupled Fluid/Solid Momentum, Energy, Mass, and Chemical Species Transport: Developer’s Guide, 2000.
