energy

EQ = energy {Galerkin_wt} T {Interpol_fnc} <floatlist>

Description / Usage

This card provides information for solving a conservation of energy differential equation. Definitions of the input parameters are defined below. Note that <floatlist> contains five constants for the Energy equation defining the constant multipliers for each term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.

energy	Name of the equation to be solved.
{Galerkin_wt}	Two- or four-character value that defines the type of weighting function for this equation, where: Q1-Linear Q2-Quadratic Q1_D-Standard linear interpolation with special allowance for discontinuous degrees of freedom at interfaces. Q2_D-Standard quadratic interpolation with special allowance for discontinuous degrees of freedom at interface. Q1_XV-Linear interpolation with enrichment in elements of material interfaces. This enrichment function allows discontinuity in value and gradient along interface but maintains continuity at element edges/faces.Only used for level-set problems. Q2_XV-Quadratic interpolation with enrichment in elements of material interfaces. This enrichment function allows discontinuity in value and gradient along interface but maintains continuity at element edges/faces. Only used for level-set problems. Q1_GN-Linear interpolation for capturing variables defined on the negative side of the level-set interface. Similar to Q1_XV. Q2_GN-Quadratic interpolation for capturing variables defined on the negative side of the level-set interface. Similar to Q1_XV
T	Name of the variable associated with this equation.
{Interpol_fnc}	Two- or four-character value that defines the interpolation function used to represent the variable T, where: Q1-Linear Continuous Q2-Quadratic Continuous Q1_D-Standard linear interpolation with special allowance for discontinuous degrees of freedom at interfaces. Q2_D-Standard quadratic interpolation with special allowance for discontinuous degrees of freedom at interfaces. Q1_XV-Linear interpolation with enrichment in elements of material interfaces. This enrichment function allows discontinuity in value and gradient along interface but maintains continuity at element edges/faces. Q2_XV-Quadratic interpolation with enrichment in elements of material interfaces. This enrichment function allows discontinuity in value and gradient along interface but maintains continuity at element edges/faces. Q1_GN-Linear interpolation for capturing variables defined on the negative side of the level-set interface. Similar to Q1_XV. Q2_GN-Quadratic interpolation for capturing variables defined on the negative side of the level-set interface. Similar to Q1_XV. Q1_GP-Linear interpolation for capturing variables defined on the positive side of the level-set interface. Similar to Q1_XV. Q2_GNP-Quadratic interpolation for capturing variables defined on the positive side of the level-set interface. Similar to Q1_XV.
<float1>	Multiplier on mass matrix term ( d ⁄dt ).
<float2>	Multiplier on advective term.
<float3>	Multiplier on boundary term ( \(\underline{n}\) • flux ).
<float4>	Multiplier on diffusion term.
<float5>	Multiplier on source term.

Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.

Examples

The following is a sample card that uses a linear continuous interpolation and weight function and has all the term multipliers on except the mass matrix term for time derivatives:

EQ = energy   Q1 T Q1   0. 1. 1. 1. 1.

Technical Discussion

Some discussion on the XFEM-type enriched basis functions Q1_XV, Q1_GN, Q1_GP, Q2_GN, Q2_GP and Q2_XV is in order. First of all, these basis functions are to be use with the level-set front tracking capability only. First of all, these basis functions are typically only used for the continuity equation to capture pressure jumps due to surface tension. However, for phase change problems some experimentation has been pursued with the energy equation.

XFEM Value Enrichment

Enrichment:

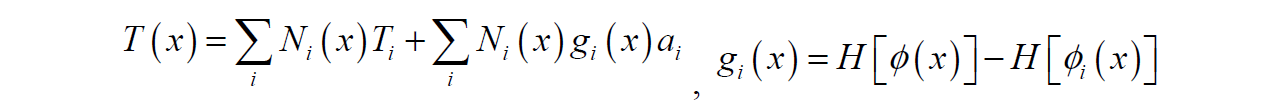
Related “Ghost” Enrichment:

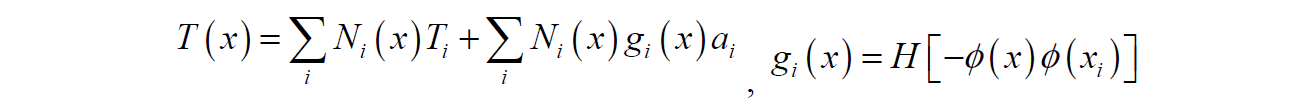
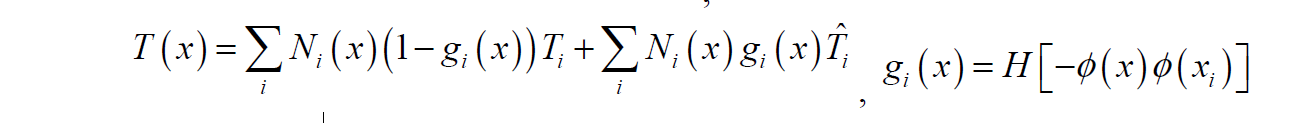
Advantages:

This enrichment function allows discontinuity in value and gradient along interface but maintains continuity at element edges/faces. Appears to be method of choice for Pressure discontinuity. Produces interface integral for terms integrated by parts that allows for specifying a weak integrated conditions. This is needed in the laser welding heat transfer problem.