Gravity-based Diffusivity#
Gravity-based Diffusivity = {model_name} <species> {float_list}
Description / Usage#
This card is used to specify Dg when the model in the Diffusivity card is HYDRO. There are two {model_name} options for this mode; definitions of the input parameters are as follows:
CONSTANT |
constant gravity-based diffusivity.
|
RICHARDSON_ZAKI |
constant gravity-based diffusivity.
|
Examples#
The following is a sample input card:
Gravity-based Diffusivity = CONSTANT 0 8.88e-7
Gravity-based Diffusivity = RICHARDSON_ZAKI 0 8.88e-7 5.1
Technical Discussion#
When a suspension of particles settles or floats in a fluid, particle-particle interactions serve to slow the terminal velocity of all the particles relative to the Stokes velocity. The terminal velocity is then corrected by what is known as the hindered settling function. If a CONSTANT model is chosen, the form of this function is
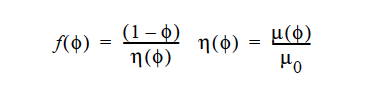
where φ is the volume fraction of suspension, η(φ) is the relative viscosity of the mixture, μ0 is the viscosity of the pure fluid.
On the other hand if RICHARDSON_ZAKI is chosen for the function,
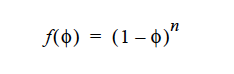
where n is the exponent specified by the user. n=5.1 has been found to fit well for suspensions of monodisperse spherical particles at low Reynolds number by Garside and Al-Dibouni (1977). Richardson-Zaki approach will not yield a zero f(φ) if φ approaches maximum packing, so it is recommended that CONSTANT is used.
References#
GTM-010.0: The Hindered Settling Function for a Glass Microballoon Suspension, March 3, 1999, C. A. Romero.
Garside, J. and M.R. Al-Dibouni, “Velocity-voidage relationship for fluidization and sedimentation in solid-liquid systems,” Ind. Eng. Chem. Process Des. Dev., 16, 206 (1977).
